Feladat:	1451. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Füzet:	1973/november, 144 - 145. oldal		PDF  |  MathML
Témakör(ök):	Egyenletek grafikus megoldása, Abszolútértékes egyenlőtlenségek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1973/január: 1451. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. $\begin{array}{c}{\displaystyle \frac{2x}{|x-3|-5}+\frac{1}{x+2}\ge 1\mathrm{.}}\end{array}$ (1) Az $|x-3|$ tag föllépése miatt két esetet kell megkülönböztetnünk. I. Ha $x-3\ge 0$, azaz $x\ge 3$, akkor (1) első törtje írható így is: $\begin{array}{c}{\displaystyle \frac{2x}{x-3-5}=2+\frac{16}{x-8}\mathrm{,}}\end{array}$ és ezzel (1) így alakítható: $\begin{array}{c}{\displaystyle \frac{16}{x-8}\ge -1-\frac{1}{x+2}\mathrm{.}}\end{array}$ (2) A jobb oldal nevezőjére $x+2\ge 5$, ezért az egész intervallumban $\begin{array}{c}{\displaystyle -1>-1-\frac{1}{x+2}\ge -1-\frac{1}{5}=-1\mathrm{,}2.}\end{array}$ (3) A bal oldal zérushelye viszont kettéválasztja az intervallumot. Ha $\begin{array}{c}{\displaystyle x>\mathrm{8,}}\end{array}$ ($*$) akkor a bal oldal pozitív, ez tehát (2) és (3) szerint megoldása az egyenlőtlenségnek. Ha ellenben $3\le x<8$, akkor a bal oldal negatív, és legnagyobb értéke $x=3$ esetén $-3\mathrm{,}2$, eszerint ebben a részintervallumban nincs megoldás. II. Az $x<3$ esetben (1) két tagjának a nevezője közösnek adódik: $\begin{array}{c}{\displaystyle \frac{2x}{-x+3-5}+\frac{1}{x+2}=\frac{1-2x}{x+2}\ge 1\mathrm{,}}\end{array}$ (4) más szóval: a bal és jobb oldal különbsége nem lehet negatív: $\begin{array}{c}{\displaystyle \frac{1-2x}{x+2}-1=\frac{-1-3x}{x+2}\ge 0\mathrm{,}}\end{array}$ vagyis a számlálónak és a nevezőnek egyenlő előjelűnek kell lennie, megengedve még azt is, hogy a számláló $0$ legyen. A számláló is, a nevező is a vizsgált intervallumban vált előjelet, a számláló a $-\frac{1}{3}$ helyen áthaladva pozitívból negatívra változik, a nevező a $\left(-2\right)$ helyen áthaladva negatívból pozitívvá lesz, így (4) a köztük levő $\begin{array}{c}{\displaystyle -2<x\le -\frac{1}{3}}\end{array}$ ($**$) értékekre teljesül. Részletezve lásd e táblázaton:   ${\displaystyle \begin{array}{cccc}{\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mi>a</mi><mi>k</mi><mi>k</mi><mi>o</mi><mi>r</mi><mo stretchy="false">-</mo></mphantom></math>ha }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false"><</mo><mo stretchy="false">-</mo><mn>2</mn></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>2</mn><mo stretchy="false"><</mo><mi>x</mi><mo>≤</mo><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>3</mn></mrow></mfrac></mrow><mo stretchy="false"><</mo><mi>x</mi><mo stretchy="false"><</mo><mn>3</mn></math>}}\hfill \\ {\displaystyle \text{akkor <math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1</mn><mo stretchy="false">-</mo><mn>3</mn><mi>x</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">></mo><mn>0</mn></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>≥</mo><mn>0</mn></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false"><</mo><mn>0</mn></math>}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mi>a</mi><mi>k</mi><mi>k</mi><mi>o</mi><mi>r</mi><mo stretchy="false">-</mo><mn>1</mn></mphantom></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false">+</mo><mn>2</mn></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false"><</mo><mn>0</mn></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">></mo><mn>0</mn></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">></mo><mn>0</mn></math> }}\hfill \end{array}}$   Ezek szerint (1) megoldásai a $\left(*\right)$ és $\left(**\right)$ értékek.       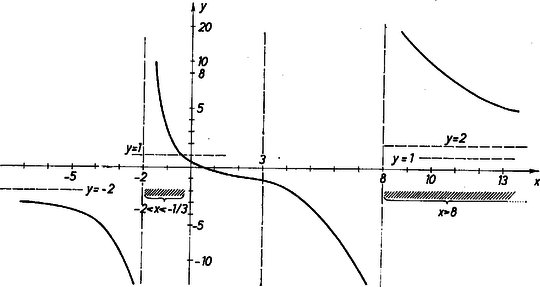Megjegyzés. (1) bal oldalának változását grafikonunk mutatja. A görbe az $x=3$ pontban folytonos, mert ott $x-3$ folytonos, de törése van.