Kezdőlap


Feladat:	1449. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1973/november, 141 - 142. oldal		PDF \| MathML
Témakör(ök):	Vetítések, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Magasságvonal, Hossz, kerület, Párhuzamos szelők tétele, Gyakorlat
Hivatkozás(ok):	Feladatok: 1972/december: 1449. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az egyenlő szárú háromszög alapját $a$ -val, a hozzá tartozó magasságot $m$ -mel, a magasság talppontját $F$ -fel, a harmadoló pontokat $B$ -től $A$ felé haladva $H_{1}$ , $H_{2}$ -vel, az alapra való merőleges vetületüket $H'_{1}$ , $H'_{2}$ -vel, $C$ pontnak $H_{1}$ és $H_{2}$ -től való távolságát $p$ -vel és $q$ -val, a keresett távolságot $x$ -sze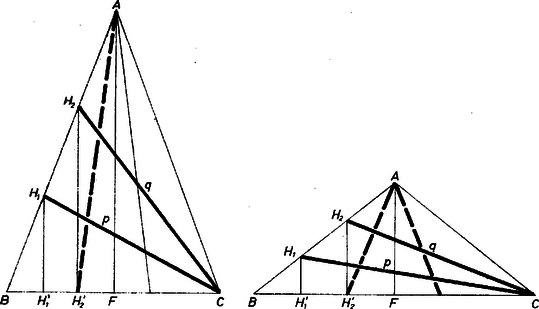l.

A párhuzamos szelők tételéből következik, hogy

B H'_{2} = \frac{2}{3} B F

, a szimmetria miatt

B F = \frac{1}{2} B C

, így

B H'_{2} = \frac{1}{3} B C

, tehát

A H'_{2} = x

.
Ugyancsak a párhuzamos szelők tételéből adódik, hogy

B H'_{1} = \frac{1}{6} a

F H'_{2} =

= \frac{1}{6} a

H_{1} H'_{1} = \frac{1}{3} m

H_{2} H'_{2} = \frac{2}{3} m

. A

H_{1} C H'_{1}

H_{2} C H'_{2}

H'_{2} A F

derékszögű háromszögekre alkalmazva Pitagorasz tételét:

\begin{matrix} p^{2} = {(\frac{1}{3} m)}^{2} + {(\frac{5}{6} a)}^{2}, q^{2} = {(\frac{2}{3} m)}^{2} + {(\frac{2}{3} a)}^{2}, x^{2} = m^{2} + {(\frac{1}{6} a)}^{2} . \end{matrix}

Az egyenleteket egyszerűbb alakra hozzuk:

\begin{matrix} 36 p^{2} & = 4 m^{2} + 25 a^{2}, & (1) \\ 9 q^{2} & = 4 m^{2} + 4 a^{2}, & (2) \\ 36 x^{2} & = 36 m^{2} + a^{2} . & (3) \end{matrix}

Mivel mindhárom egyenlet jobb oldalán csak

m^{2}

-es és

a^{2}

-es tag áll, kereshetünk olyan

λ

és

μ

számot, amellyel (1)-et, illetve (2)-t szorozva és összeadva, a jobb oldalon mindjárt éppen (3) jobb oldalát kapjuk.

m^{2}

és

a^{2}

együtthatói alapján

\begin{matrix} 4 λ + 4 μ = & 36, \\ 25 λ + 4 μ = & 1, \end{matrix}

innen kivonással tüstént

λ = - \frac{35}{21} = - \frac{5}{3}

, és tovább az elsőből

μ = 9 - λ = \frac{32}{3}

ilyen szorzók. Valóban, (1)-et

- \frac{5}{3}

-dal, (2)-t

\frac{32}{3}

-dal szorozva és összeadva

\begin{matrix} 96 q^{2} - 60 p^{2} = 36 m^{2} + a^{2} = 36 x^{2} . \end{matrix}

Ahonnan rögtön kapjuk, hogy

x^{2} = (8 q^{2} + 5 p^{2}) / 3

.
A feladat nem adja meg közelebbről a 17 és 20 távolságok szerepét, ezért a

p = 17

q = 20

és a

p = 20

q = 17

esetek mindegyike lehetséges. Az elsőben

x_{1} = \sqrt[]{585} \approx 24, 2

cm, a másodikban

x_{2} = \sqrt[]{104} \approx 10, 2

cm. Mindkét eredmény eleget tesz a kívánt feltételeknek.