Feladat: 1444. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bagó Balázs ,  Baranyi József ,  Böősi Imre ,  Gáspár Gyula ,  Józsa János ,  Kelemen Gábor ,  Markó Péter ,  Nagy János ,  Strommer Pál ,  Vass Albert (Debrecen) 
Füzet: 1973/december, 208 - 211. oldal  PDF  |  MathML 
Témakör(ök): Játékelmélet, játékok, Téglalapok, Négyzetek, Gyakorlat
Hivatkozás(ok):Feladatok: 1972/december: 1444. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Megmutatjuk, hogy a terv nem hajtható végre. Elég evégett tekinteni a táblázatnak egy 4×12-es téglalapját, vagyis 4 egymás alatti sorából és 12 egymás utáni oszlopából alakuló téglalapját, sőt ebben is csak a beírandó 2-es számjegyeket. Föltesszük, hogy ezek beírhatók a követelmények szerint.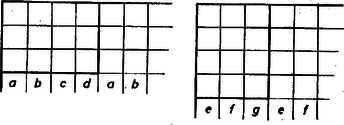
Vágjunk ki egy átlátszatlan papírlapból egy 3×4 mezőnyi téglalap alakú ablakot, helyezzük azt fekvő helyzetben a táblázat bal felső sarkába és jelöljük a 4 látható (3 mezőnyi magas) oszlopban álló 2-esek számát rendre a, b, c, d-vel. Így az előírás szerint

a+b+c+d=5,
tehát a, b, c, d közül legalább egynek legalább 2 az értéke.
 

 

1. ábra
 

Az ablakot 1 oszloppal jobbra tolva balról eltűnik a db 2-es, de ugyanennyi megjelenik a jobbról következő oszlopban (1. ábra a) része). Ezt folytatva kapjuk, hogy a felső három sor oszlopaiban a 2-esek száma négytagú szakaszokban ismétlődik.
Megismételve eljárásunkat álló helyzetű ablakkal (1. ábra b) része), legyen az első 3 látható (4 mezőnyi magas) oszlopban talált 2-esek száma rendre e, f, g, így
e+f+g=5,(1)
és az ablakot 1‐1 mezőnyivel jobbra tolva, a balról eltűnő 2-esek helyett minden lépésben ugyanannyit találunk az újabb és újabb láthatóvá váló oszlopokban, tehát a 2-esek szám háromtagú szakaszokban ismétlődik.
12 oszloppal jobbra lépve teljes szakasz fejeződik be a, b, c, d-ből is, e, f, g-ből is. Egymás fölé-alá írva oszloponként az első három, illetve az első négy sorban álló 2-es jegyek számát:
  a,    b,    c,    d,    a,    b,    c,    d,  a,    b,    c,    d,    e,    f,    g,    e,    f,    g,    e,    f,    g,    e,    f,    g,  

nyilvánvaló, hogy az alsó szám sehol sem kisebb a fölötte állónál.
Mármost az e, f, g betűk mindegyike föllép az a, b, c, d betűk mindegyike alatt, az utóbbiak közül viszont legalább az egyik legalább 2, tehát e, f, g mindegyike legalább 2. Így pedig nem teljesülhet (1); állításunkat bebizonyítottuk.
 

Böősi Imre (Győr, Czuczor G. Bencés Gimn., II. o. t.)
 

II. megoldás. A táblázatban bárhol választott 3×3 mezős négyzetet legalább két oldala mentén lehet toldani 3×4-es, illetve 4×3-as téglalappá (2. ábra a) része), egy-egy 3×1-es, illetve 1×3-as téglalappal. Mind a két kis téglalapban ugyanaz a három számjegy áll valamilyen sorrendben, hiszen mind a két kis téglalap ugyanannak a négyzetnek a számjegykészletét egészíti ki az előírás szerintire.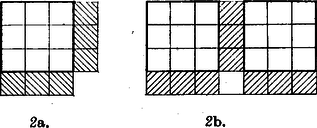
 

 


Ezek alapján vizsgáljuk a 2b ábra vonalkázott részeivel egyidejűleg lefedhető, egymással egyező jegyek kapcsolatait (hiszen az álló téglalap közvetítésével az ábra két fekvő téglalapjában is ugyanaz a három jegy áll valamilyen sorrendben).
 

 

3. ábra
 

Tegyük rá a táblázatra a 3. ábrát úgy, hogy az M mező egy 0 jegyre essék és A, K, S is fedjenek egy-egy jegyet. Ha most a 2a ábra bal alsó 1×3-as téglalapját egymás után a KLM, LMN, MNP mezőhármasra tesszük rá, rendre kapjuk, hogy az ADG, a BEH, a CFJ mezőhármasokon van 0 jegy. És mivel az A, C, R, N sarokmezőkkel meghatározott téglalapban együttvéve 3 db van, azért N, P, R egyikén sem áll 0.
Másrészt a 2b ábra hal oldali fekvő téglalapját a KLM mezőkre téve adódik, hogy a P, R, S mezők egyikén 0 áll. Ez az előbbi eredmény alapján csak S lehet. Eszerint amelyik sorban van 0, abban 4 mezővel jobbra lépve is 0-t találunk és közben nincs 0; továbbá a táblázat határától elég távol kijelölt 3×1-es és 1×3-as téglalapban legföljebb egy db 0 található.
Az 1-esekre térve, nem fedhet L, M mindegyike 1-est, mert akkor A, D, G közt is, B, E, H közt is két-két 1-es volna és a BPM csúcsú ablakban öt 1-est látnánk. Hasonlóan nem fedhet 1-eseket az L, N pár sem, mert akkor a BH oszlopban két, az AG, CJ oszlopokban egy-egy db 1-es lenne (L, illetve N miatt), és az ACRN ablakban legalább 5 lenne.
Ezek szerint, ha M1-est fed, de K, L, N, P egyike sem. akkor az ACJG négyzet mindhárom oszlopában egy-egy db 1-es áll, az ACRN ablakban pedig négy db, ezért R is 1-est fed, tehát az M során végigmenve, az 1-esek hármasával ismétlődnek. Azt is kaptuk itt, hogy M, N, P, R oszlopában van 1-es, így minden oszlopban van, tehát minden sorban is, hiszen táblázatunkat 90∘-kal elfordítva; oszlopai sorokká válnak és tulajdonságai megmaradnak.
Végül a 2-esekről ezt kapjuk: nem fedhet K, L, M mindegyike 2-est, mert akkor már az ACJG négyzet hat db-ot tartalmaz belőle.
Eszerint ha egy sorban van 0 jegy, akkor a két legközelebbi 0 közti három hely valanelyikén van 1-es, de csak egyen.
A talált szabályszerűségek szükséges föltételei a táblázat kitölthetőségének. Legyen az i-edik sor olyan, amely tartalmaz 0-okat (4≦i≦50). Jelölhetjük e 0-ok oszlopainak sorszámát így: k,(k+4),(k+8),(k+12),..., ahol 3≦k≦50. Akárhogy választjuk mármost az (i,k) és (i,k+4) mezők közti 1-es oszlopának sorszámát, tőle jobbra haladva hármasával, előbb - utóbb olyan mezőre kellene írnunk 1-est ahol már 0 áll: ha 1-es áll
az(i,k+1)-en,akkor az(i,k+4)-en is,az(i,k+2)-n,akkor az(i,k+8)-on is,az(i,k+3)-on,akkor az(i,k+12)-n is,
Eszerint a kapott szükséges föltételek közt ellentmondás van, a táblázat kívánt kitöltése lehetetlen.
 

Bagó Balázs (Győr, Révai M. Gimn., II. o. t.)
 

III. megoldás. A II. megoldás szemléletes elemeire támaszkodva vázolunk egy további módot arra, hogyan ütközhetünk ellentmondásba az elrendezés folyamán.
Bármely 1×12-es téglalapban ugyanaz a számjegykészlet lép föl, mint egy, az előírásban szereplő 4×3-as vagy 3×4-es ablakban. Ugyanis egy 1×12-es téglalap létrejön úgy, hogy egy 4×12-esből elhagyunk egy 3×12-est, márpedig a 4×12-est 4 db 4×3-as ablak‐és a benne levő jegykészlet ‐ teszi ki, a 3×12-est pedig 3 db 3×4-es, továbbá mert minden 1×12-es legalább az egyik hosszabb oldala mentén kiegészíthető 4×12-essé (4. ábra).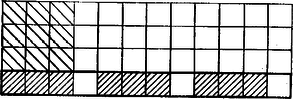
 

 

4. ábra
 

Ugyanaz a jegykészlete a 4. ábra alsó sávja három egyformán vonalkázott l×3-as téglalapjának is, a 2. ábráról mondottak alapján. Így mindegyikben egy db 0 áll-tehát az 1×12-es fehéren hagyott mezőire nem marad 0‐, hiszen különben éppen a fehér mezőkön állna a jegykészlet három 0-ja, akkor pedig a 4 db 1-es nem lenne egyenlően elosztható a három db 1×3-asba (sem az 5 db 2-es).
Kimondhatjuk ugyanezeket három db olyan 1×12-es téglalapra is, amely az eddig tekintetből fölfelé vagy lefelé 1‐1 egységnyi eltolásokkal áll elő, és ezeknek is választhatjuk a vonalkázott 1×3-asokból eredő részeit. Ekkor pedig az egymás fölötti 4‐4 db 1×3-asból alakuló 4×3 -as ablakokban 4‐4 db 0 lenne, ellentétben a feladat követelményével.
 

Megjegyzés. Az 1×12-es téglalapról mondottak azt is jelentik, hogy minden sorban és oszlopban elő kellene fordulnia mindegyikféle számjegynek.