Feladat: 1443. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1973/október, 66 - 68. oldal  PDF  |  MathML 
Témakör(ök): Vetítések, Derékszögű háromszögek geometriája, Simson-egyenes, Körülírt kör, Mértani helyek, Gyakorlat
Hivatkozás(ok):Feladatok: 1972/november: 1443. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A sík azon pontjainak mértani helye, melyeket egy AB egyenesre merőlegesen vetítve, a vetület az AB szakasz belső pontja lesz, nyilvánvalóan a szakaszra az A-ban és B-ben állított merőleges egyenesek közti síksáv. A merőlegesek pontjai nem tartoznak hozzá a mértani helyhez (1. ábra).

 

 

1. ábra
 

Legyen k egy, az A-n és B-n átmenő kör, és messe ezt a mondott síksáv A-n átmenő határa B*-ban, a B-n átmenő határa A*-ban. Ekkor a k-ból a félkörnél kisebb AB*, BA* ívekre eső pontoknak ‐ a végpontokat is hozzáértve ‐ az AB egyenesen levő vetülete nem belső pontja az AB szakasznak. Thalész tétele alapján AA* és BB* a k-nak átmérői. A mondott ívek csak akkor zsugorodnak össze egy-egy pontra, ha AB a k-nak átmérője. (A továbbiakban ‐ ha körívet mondunk ‐ mindig a félkörnél nem hosszabb ívet értjük.)
Vegyük hozzá most A-hoz és B-hez k-nak C pontját, és legyen C* a C-vel átellenes pont. Ekkor az előbbiekhez hasonlóan nem belső pont a vetülete az ABC háromszög
ABoldalegyenesén azAB*ésBA*ívek pontjainak,BColdalegyenesén aBC*ésCB*ívek pontjainak,(1)CAoldalegyenesén aCA*ésAC*ívek pontjainak;

(az egyes egyenesek mellett nem említett ívek belső pontjaira nézve viszont a vetület belső pont lesz a megfelelő oldalszakaszon mint pl. AB-n az AB és A*B* ívek pontjaié.) Így már csak azt kell belátnunk, hogy az (1) alatti 6 ív együttvéve lefedi k-nak minden pontját, kizárja rájuk a 3 elemű tulajdonságnak legalább egy elemét.
Valóban, ha az ABC háromszög hegyesszögű, azaz C a félkörnél kisebb A*B* íven van, akkor az íveket határoló pontok sorrendje A, C*, B, A*, C, B*, így k-nak minden pontja éppen egy (1) alatti ívhez, a 6 pont pedig két-két ívhez tartozik hozzá (2a. ábra);
 

 

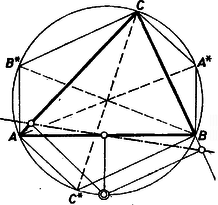2a. ábra
 

ha van a háromszögben derékszög ‐ válaszszuk C-t a csúcsául, ‐ akkor B* azonos A-val és A* azonos B-vel, ekkor hasonlóan (1)-ből az utolsó négy ív fedi le k-t (2b. ábra);
 

 

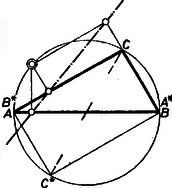2b. ábra
 

ha pedig van tompaszög ‐ legyen ACB∢>90∘, vagyis ha C az AB íven van ‐, akkor pontjaink egymásutánja A, B*, C*, A*, B, C, tehát az A pont belső pontja a CB* ívnek, továbbá B*, A*,B belső pontja rendre az AC*-nak, a BC*-nak, a CA*-nak és az (1) ívek ekkor is lefedik k-nak minden pontját, sőt az AB*, BA* ívek pontjait háromszor is (2c. ábra). ‐ Más eset nincs, ezzel bizonyításunkat befejeztük.
 

 

2c. ábra
 
 

Megjegyzések. 1. A kitűzött állítás bizonyítása mellett tulajdonképpen megkaptuk a háromszög síkjának azokat a pontjait, melyeknek a vetülete mindhárom oldalszakaszon belső pont; mondjuk is ki az eredményeket. Ezek a pontok a következő idomok belső pontjai: a 2a. ábrán az AC*BA*CB* konvex, centrálszimmetrikus hatszög, a 2b. ábrán az ACBC* téglalap, a 2c. ábrán a CDC*E paralelogramma.
2. Többen bizonyításul a Simson-féle, más néven Wallace-féle egyenesek tételére* hivatkoztak. Ez a tétel azt mondja ki a háromszög körülírt körének pontjairól, hogy a szóban forgó 3 vetületük egy egyenesen van. Mivel pedig egy egyenesnek a háromszög kerületével legfeljebb két közös pontja lehet, azért az állítás helyes. Ez az érvelés helyes, legfeljebb az a szépséghibája, hogy magánál az állításnál jóval erősebb tételre hivatkozik, "nagy ágyút'' használ.
*Lapunkban legutóbb a P. 108. problémában szerepelt, K. M. L. 46 (1973) 71‐73. old.