Feladat: 1423. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1973/március, 111 - 113. oldal  PDF  |  MathML 
Témakör(ök): Valós számok és tulajdonságaik, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Téglalapok, Egyéb sokszögek geometriája, Gyakorlat
Hivatkozás(ok):Feladatok: 1972/május: 1423. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A vizsgálandó ABCDE ötszög 90∘-os szögei közül kettőnek a csúcsa mindenesetre szomszédos, jelöljük ezeket A-val és B-vel, éspedig úgy, hogy A másik szomszédja, E, az egyik 135∘-os szög csúcsa legyen. Ekkor feladatunk a további két szög- és az oldalmértékszámok szerepének megállapítása. A harmadik derékszög csúcsa vagy C, vagy D. Mindenesetre a BC és AE oldalegyenesek párhuzamosak, mert mindkettő merőleges AB-re, és a konvexség alapján D köztük van.

 

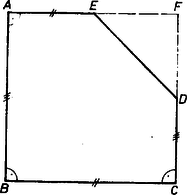
I. Ha BCD∢=90∘, tehát CDE∢=DEA∢=135∘, akkor még AB∥CD, és E köztük van (1. ábra).
 

 

1. ábra
 

Az AE, CD egyenesek metszéspontját F-fel jelölve D a CF szakaszon, E pedig az AF szakaszon van, tehát
AE<AF=BC,CD<CF=AB,(1)
hiszen ABCF téglalap. Továbbá DEF egyenlő szárú derékszögű háromszög, mert D-nél és E-nél levő külső szögei egyenlők, ezért
BC-AE=AF-AE=EF=FD=AB-CD,(2)
vagyis ötszögünk négy oldalából alakított két oldalpár különbsége egyenlő.
 

Nem szerepelhet e négy oldal mértékszámai közt a 2, az adatok közti egyetlen irracionális mértékszám, különben a (2) egyenlőség egyik oldalán irracionális szám állna, a másikon racionális szám, ami lehetetlen. Így 2 csak az (1)-ben nem szereplő DE oldal hossza lehet, vagyis a DEF háromszög átfogójáé. Ezért EF=DF=1, ennélfogva (1)-re tekintettel BC=BA=2 és AE=CD=1.
A méretek szerepének ezen elosztása nyilvánvalóan megoldását adja a feladatnak, az ötszög egy 2 egységnyi oldalú négyzetből áll elő, egyik sarkának a mondott méretek szerinti levágásával.
 

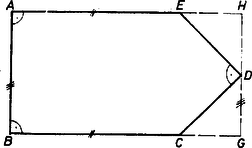
II. Ha pedig CDE∢=90∘, és így BCD∢=DEA∢=135∘, akkor húzzunk párhuzamost D-n át AB-vel, és messe ez a BC egyenest G-ben, az AE egyenest H-ban (2. ábra).
 

 

2. ábra
 

Így a DCG háromszögben G-nél derékszög van, ezért C-nél levő szöge nem lehet 135∘, tehát C a BG szakaszon van; és DCG∢=45∘, DG=CG; ugyanígy E az AH szakaszon van és DH=EH. Ezek szerint CDG, EDH egyenlő szárú derékszögű háromszögek, és
AB=GH=GD+DH=CD2+DE2.(3)
Itt sem CD, sem ED hossza nem lehet 2. Különben ugyanis a jobb oldal egyik tagja 1, azaz racionális szám lenne, a másik tag irracionális, és a bal oldal hossza is csak racionális számok közül volna választható. Eszerint a (3)-ból átszorzással adódó
2⋅AB=CD+DE
egyenlőség jobb oldala egész, az egyenlőség csak AB=2 mellett teljesülhet, tehát CD+DE=2, ez pedig a további 4 szakaszból csak úgy állítható elő, ha mindkét tagja 1; végül BC=AE=2. Ezt a megoldást is egyértelműen kaptuk, más megoldása nincs a feladatnak.
 

Megjegyzések. 1. A fentiekben azt használtuk fel, hogy egy racionális és egy irracionális szám összege nem lehet racionális szám.
2. Ötszögünk konvex voltát tulajdonképpen már a szögek adott értéke biztosította, de felhasználtuk, hogy egy konvex sokszög bármelyik oldalegyeneséhez képest az egyik parton helyezkedik el. Meg lehet mutatni, hogy ez az értelmezés egyenértékű a tankönyv* fogalomalkotásával.
*Horvay K.‐Pálmay L. Matematika a gimn. I. o. számára. Tankönyvkiadó Budapest, 1966. 199. old.