Kezdőlap


Feladat:	1417. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1974/november, 131 - 132. oldal		PDF \| MathML
Témakör(ök):	Középpontos tükrözés, Eltolás, Transzformációk szorzata, Magasságvonal, Körülírt kör, Magasságpont, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1972/április: 1417. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1371. gyakorlat szövege a következő volt: Az $A B C$ háromszög magasságvonalainak talppontjai rendre $A_{1}$ , $B_{1}$ , $C_{1}$ . Adva van (helyzet szerint) az $A B_{1} C_{1}$ , a $B C_{1} A_{1}$ és a $C A_{1} B_{1}$ háromszög magasságpontja. Szerkesszük meg a háromszöget. ‐ A megoldás menete a következő volt. Jelöljük az adott magasságpontokat ( $H_{2}$ csúcsait) rendre $A_{2}$ -vel, $B_{2}$ -vel és $C_{2}$ -vel, a $H_{2}$ háromszögbe írható kör középpontját $O$ -val, a háromszöghöz hozzáírható körök középpontjait $O_{a}$ -val, $O_{b}$ -vel és $O_{c}$ -vel. Tükrözzük az $O$ pontot a $B_{2} C_{2}$ szakasz felezőpontjára, a kapott pontot jelöljük $T$ -vel, és az $O_{a}$ , $O_{b}$ , $O_{c}$ pontokat tükrözzük az $A_{2} T$ szakasz $F$ felezőpontjára: a kapott három tükörkép lesz a keresett háromszög három csúcsa. További megoldásokat kapunk, ha $O$ helyére az $O_{a}$ , $O_{b}$ , $O_{c}$ valamelyikét választjuk, és a választott pont helyére $O$ -t tesszük. A jelen feladatunk megoldásának az alapgondolata az lesz, hogy megvizsgáljuk, milyen következményekkel jár ez a szerepcsere.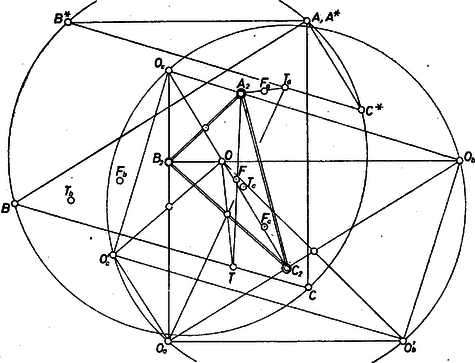
Válasszuk mondjuk $O_{a}$ -t $O$ helyett: $O_{a}$ -nak a $B_{2} C_{2}$ szakasz felezőpontjára vonatkozó tükörképe legyen $T_{a}$ , és az $A_{2} T_{a}$ szakasz felezőpontja legyen $F_{a}$ . Ekkor a keresett háromszög csúcsai az $O$ , $O_{b}$ , $O_{c}$ pontoknak az $F_{a}$ -ra vonatkozó tükörképei lesznek.

1. ábra

T

és

F

pontok szerkesztése szerint

\begin{matrix} \vec{O F} = \frac{1}{2} ({\vec{O A}}_{2} + \vec{O T}) = \frac{1}{2} ({\vec{O A}}_{2} + {\vec{O B}}_{2} + {\vec{O C}}_{2}), \end{matrix}

amint ezt már az 1371. gyakorlat megoldása során megjegyeztük. Hasonlóan látható, hogy

\begin{matrix} {\vec{O_{a} F}}_{a} = \frac{1}{2} ({\vec{O_{2} A}}_{2} + {\vec{O_{a} B}}_{2} + {\vec{O_{a} C}}_{2}), \end{matrix}

tehát

\begin{matrix} {\vec{F F}}_{a} = {\vec{O F}}_{a} - \vec{O F} = {\vec{O O}}_{a} + ({\vec{O_{a} F}}_{a} - \vec{O F}) = {\vec{O O}}_{a} - \frac{3}{2} {\vec{O O}}_{a} = - \frac{1}{2} {\vec{O O}}_{a} . \end{matrix}

Ismeretes, hogy egy tetszőleges

P

pontnak az

F_{a}

-ra vonatkozó tükörképét úgy is megkapjuk, ha előbb eltoljuk a

2 \vec{F_{a} F}

vektorral, majd tükrözzük a kapott pontot

F

-re. Alkalmazzuk ezt az eljárást az

O

O_{b}

O_{c}

, pontokra: toljuk el először őket a

2 \vec{F_{a} F} = \vec{O O_{a}}

vektorral, és a kapott pontokat tükrözzük

F

-re. Az eltolás

O

-t

O_{a}

-ba,

O_{b}

-t és

O_{c}

-t pedig azokba az

O'_{b}

O'_{c}

pontokba viszi, amelyekre (2. ábra)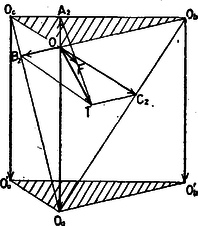

\begin{matrix} {\vec{O O}}_{a} = {\vec{O_{b} O'}}_{b} = {\vec{O_{c} O'}}_{c}, \end{matrix}

tehát amelyeket

O

-nak az

O_{a} O_{b}

O_{a} O_{c}

szakaszok felezőpontjára való tükrözésével is megkaphatunk.

2. ábra

Mivel

O

O_{a} O_{b} O_{c}

háromszög magasságpontja, azért

O'_{b}

O'_{c}

rajta van az

O_{a} O_{b} O_{c}

háromszög köré írható körön, vagyis az

O_{a} O_{b} O_{c}

és

O_{a} O'_{b} O'_{c}

háromszögek köré írható kör azonos. Nem változtat ezen az

F

pontra való tükrözés sem: az

O

-ból és

O_{a}

-ból kapott háromszögek (az 1. ábrán

A B C

, illetve

A^{*} B^{*} C^{*}

, ahol

A^{*}

azonos

A

-val) köré írható kör tehát azonos.
A fenti meggondolásban

O_{a}

-t

O_{b}

-vel, majd

O_{c}

-vel, felcserélve kapjuk annak a bizonyítását, hogy a másik két háromszög köré írható kör is azonos az első háromszög köré írható körrel, feladatunk állítását ezzel bebizonyítottuk.

Megjegyzés. Meg lehet mutatni, hogy a legutóbb talált

B^{*}

pont a közös körülírt körön a

B

-vel átellenes pont, a kör középpontja azonos a

H_{2}

háromszög magasságpontjával, továbbá hogy az adódott

A B C

háromszög

A

-ból induló magasságának

A_{1}

talppontja azonos

T

-vel,

A^{*} B^{*} C^{*}

-ban pedig

A^{*}

vetülete

B^{*} C^{*}

-ra azonos

T_{a}

-val.