Kezdőlap


Feladat:	1412. matematika gyakorlat	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1973/május, 211 - 213. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Pont körüli forgatás, Egyenlő szárú háromszögek geometriája, Kombinatorikai leszámolási problémák, Hossz, kerület, Szögfüggvények, síkgeometriai számítások, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1972/március: 1412. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Tekintsük az $A_{0} A_{1} ... A_{9} = S_{10}$ szabályos tízszög bármelyik $A_{i} A_{j} = d (j > i)$ átlóját. Ennek $f$ felező merőlegese átmegy az $S_{10}$ köré írt $k$ kör $O$ középpontján, így az $f$ -re való tükrözés önmagába viszi át $k$ -t, azt értve ezen, hogy $k$ pontjait páronként egymásba viszi át, $k$ és $f$ közös pontjai pedig helyben maradnak; a párokat összekötő szakaszok merőlegesek $f$ -re. Ilyen pár $A_{i}, A_{j}$ is, ezért a tükrözés $S_{10}$ -et is önmagába viszi át, és $S_{10}$ -nek további 8 csúcsa is legalább 3 ilyen párba kapcsolódik, közülük legfeljebb 2 pár alkotja $S_{10}$ -nek egy-egy oldalát, így mindenesetre marad $S_{10}$ -nek $A_{i} A_{j}$ -vel párhuzamosan legalább 1 (szoros értelemben vett) átlója, amint a feladat állítja.
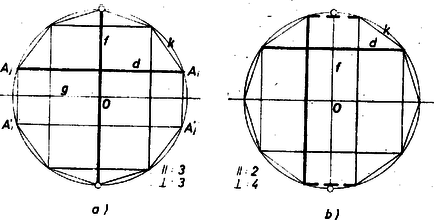
Amennyiben $k$ és $f$ közös pontjai maguk is csúcsai $S_{10}$ -nek (1a. ábra), akkor a köztük levő szakasz mindjárt egy, a $d$ -re merőleges átló; ha pedig $f$ nem átló (1b. ábra), akkor $f$ oldalfelező merőlegese $S_{10}$ -nek (mert másféle szimmetriatengelye nincs a tízszögnek), van tehát $S_{10}$ -nek két oldala, mely $f$ -re merőleges. Ezek végpontjai téglalapot határoznak meg ‐ hiszen az $O$ körüli $180^{\circ}$ -os elfordítás is önmagába viszi át a tízszöget ‐ és a téglalap további két oldala a $d$ -re merőleges átló. Ezzel az állításokat bebizonyítottuk.

1. ábra

2. Az előbbi meggondolásból adódik, hogy

f

akkor és csak akkor átlója a tízszögnek, ha a

d

-nek egyik partján levő tízszögcsúcsok

k

száma páratlan (és ekkor a másik partján levő csúcsok

8 - k

száma is páratlan, (1a. ábra). Ilyenkor az

f

-en kívül álló 8 csúcs 4 db

d

-irányú átlót alkot, tehát a

d

-vel párhuzamos, tőle különböző átlók száma 3. A

d

-re merőleges átlók

g

közös felező merőlegese viszont oldalfelező (párhuzamos

d

-vel), erre vonatkozóan a 10 csúcs 5 párt alkot, közülük 2 pár a tízszög egy-egy oldala, így páratlan

k

szám esetén a

d

-re merőleges átlók száma ugyancsak 3.
Hasonlóan

f

akkor és csak akkor oldalfelező, ha

k

páros, ekkor

d

-vel párhuzamosan 2 átló halad, rá merőlegesen pedig 4 (1b. ábra).
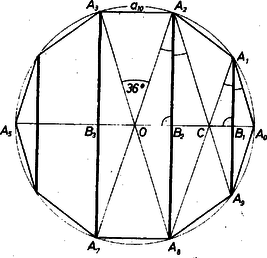
3. A 2 egységnyi

A_{0} A_{5}

átmérőt a rá merőlegesen álló 4 átló 5 részre osztja (2. ábra), közülük kettő-kettő a szimmetria folytán egyenlő egymással, a középső pedig

S_{10}

-nek vele párhuzamos

A_{2} A_{3} = a_{10}

oldalával egyenlő, ami a kitűzéskor idézett 1766. feladat^{$^{*}$} szerint

2. ábra

\begin{matrix} B_{2} B_{3} = 2 sin 18^{\circ} = \frac{\sqrt[]{5} - 1}{2} (= 0, 618); \end{matrix}

hiszen

O A_{2} A_{3}

egyenlő szárú háromszög, és a szárai közti szög

360^{\circ} : 10 = 36^{\circ}

.
Az

A_{0} A_{5}

tengelyre tükrös

A_{2} A_{7}

A_{8} A_{3}

, valamint

A_{1} A_{8}

A_{9} A_{2}

átlópárok a tengelyen metszik egymást, a kerületi szögek tétele alapján a jelölt szögek egyenlők, így az

O C A_{2}

és

C A_{0} A_{1}

háromszögek egyenlő szárúak, ezért

\begin{matrix} O C = 2 O B_{2} = B_{3} B_{2} = a_{10}, \\ B_{1} A_{0} = \frac{C A_{0}}{2} = \frac{1 - O C}{2} = \frac{3 - \sqrt[]{5}}{4} (= 0, 382), \end{matrix}

végül

\begin{matrix} B_{2} B_{1} = B_{2} C + C B_{1} = \frac{O C}{2} + \frac{C A_{0}}{2} = \frac{O A_{0}}{2} = \frac{1}{2} . \end{matrix}

Megjegyzések. 1. A

d

-vel párhuzamos átló létezésének bizonyítására egyszerű ötletnek ígérkezik ez: tükrözzük a

d = A_{i} A_{j}

átlót

O

-ra, ekkor az

A'_{j} A'_{i}

tükörkép is átló és párhuzamos

d

-vel. Így azonban külön bizonyításra van szükség arra az esetre, ha

d

éppen átmérő, hiszen ekkor a tükörkép azonos

d

-vel.
Az

A_{i} A_{j}

-re merőleges átlóként pedig

A_{i} A'_{j}

-re kézenfekvő rámutatni. De itt is marad pótolni való:

A'_{j}

azonos

A_{i}

-vel, ha

d

átmérő; lehet továbbá

A_{i} A'_{j}

oldala is a tízszögnek.
2. Az állítás és fenti bizonyításunk érvényes minden

4 n

és

(4 n + 2)

oldalú szabályos sokszögre, ha

n \geq 2

. (A bizonyítás a

4 n

oldalszám esetén kissé módosul.)

^{$^{*}$}K. M. L. 43 (1971) 15. oldal.