Kezdőlap


Feladat:	1411. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kollár János , Kovács Zoltán
Füzet:	1972/szeptember, 21 - 23. oldal		PDF \| MathML
Témakör(ök):	Beírt alakzatok, Középpontos tükrözés, Paralelogrammák, Rombuszok, Húrnégyszögek, Alakzatok köré írt kör, Gyakorlat
Hivatkozás(ok):	Feladatok: 1972/március: 1411. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az állítás egyértelmű azzal, hogy $O_{1}$ és $O_{2}$ egymás tükörképei az $O M$ szakasz $F$ felezőpontjára nézve. Ezt fogjuk bizonyítani azzal, hogy az $O_{1}$ -et, $O_{2}$ -t meghatározó oldalfelező merőlegesek közül kettő-kettő az $F$ -re tükrös párt alkot (1. ábra, az $A$ -hoz közelebbi $O'$ helyese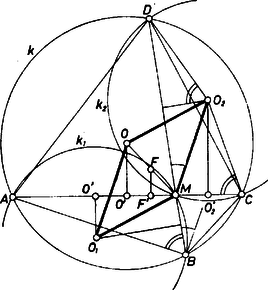n $O'_{1}$ ).

1. ábra

O_{1}

-et az

M A

M B

szakaszpár,

O_{2}

-t pedig az

M C

M D

szakaszpár felező merőlegesei metszéspontjának tekintjük, így állításunk nyilvánvalóan az

M A

M C

és az

M B

M D

párok felező merőlegeseire vonatkozik. Az

O

O_{1}

O_{2}

és

F

pont

A C

-n levő vetületét rendre

O'

-vel,

O'_{1}

-vel,

O'_{2}

-vel,

F'

-vel jelölve elég azt belátnunk, hogy

O'_{1}

-t

F'

-re tükrözve

O'_{2}

-t kapjuk. Valóban, ezek a pontok mind az

A C

szakaszon vannak, és

A

-tól mért távolságuk rendre

\begin{matrix} A O'_{1} = & \frac{1}{2} A M, \\ A F' = & \frac{1}{2} (A O' + A M) = \frac{1}{4} A C + \frac{1}{2} A M, \\ A O'_{2} = & \frac{1}{2} (A M + A C), \end{matrix}

amiből

A F' = \frac{1}{2} (A O'_{1} + A O'_{2})

következik.

Ugyanígy bizonyítható, hogy

M B

és

M D

felező merőlegese tükrös az

F

pontra, tehát a feladat állítása az előrebocsátottak szerint helyes.

Egyszerűsítéssel Kovács Zoltán (Győr, Révai M. Gimn., II. o. t.) dolgozatából.

II. megoldás. Az

O O_{1} M O_{2}

négyszög

O O_{1}

oldala szerkesztésnél fogva az

A B

szakasz felező merőlegese. Erre tekintettel azt fogjuk bizonyítani, hogy az

O_{2} M

egyenes is merőleges

A B

-re, hiszen így párhuzamos

O O_{1}

-gyel. Ez az eredeti ábrából minden hozzáadás nélkül adódik akkor, ha

A D

O

középpontú körnek átmérője (2. ábra), hiszen ekkor

M D ⊥ A B

O_{2}

pedig az

M D

szakasz felezőpontja, mert

M D C

derékszögű háromszög, és

M D

az átfogója.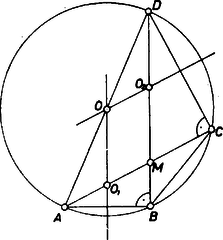

2. ábra

A D

nem átmérő, akkor az

M C D ∢ = A C D ∢

nem derékszög,

O_{2}

nincs az

M D

-n, az

O_{2} M D

egyenlő szárú háromszögből

\begin{matrix} D M O_{2} ∢ = (180^{\circ} - D O_{2} M ∢) / 2 = 90^{\circ} - D O_{2} M ∢ / 2. \end{matrix}

(1)

A kivonandó mindenesetre hegyesszög és egyenlő a

D C M \equiv D C A

D B A

szögekkel, hacsak ezek hegyesszögek (1. ábra), tehát az utolsó alak a

D B A

szög pótszöge,

M O_{2}

párhuzamos az

A B

-re

B

-ben állított merőlegessel,

M O_{2}

merőleges

A B

-re, mert

M C D ∢ < 90^{\circ}

alapján

O_{2}

azon a partján van a

B D

egyenesnek, mint

C

, az

A

pont pedig a másik partján.
Ha pedig a

D C M \equiv D C A

D B A

szögek tompaszögek, akkor kiegészítő szögük egyenlő (1) kivonandójával, vagyis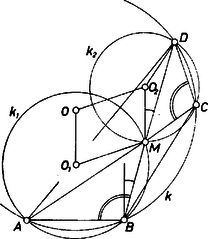

\begin{matrix} D M O_{2} ∢ = 90^{\circ} - (180^{\circ} - D B A ∢) = D B A ∢ - 90^{\circ} \end{matrix}

és most az

A

és

O_{2}

pontok a

B D

egyenesnek ugyanazon az oldalán vannak, tehát

M O_{2}

ekkor is párhuzamos a

B

-ben

A B

-re állított merőlegessel (3. ábra).

3. ábra

Írjunk most ábráink

A

B

C

D

betűje helyére rendre

C

D

A

B

betűt, ekkor

O_{1}

helyére

O_{2}

-t és

O_{2}

helyére

O_{1}

-et kell írnunk és fenti bizonyításunk szerint az új

O O_{1}

és új

O_{2} M

párhuzamosak, vagyis az eredeti

O O_{2}

és

O_{1} M

párhuzamosak. Így pedig

O O_{1} M O_{2}

valóban paralelogramma.
A paralelogramma

O O_{2}

oldalegyenese a

C D

oldal felező merőlegese.

Ha az

A B C D

négyszögben

A B

párhuzamos

C D

-vel, akkor felező merőlegesük azonos és a vizsgált paralelogramma elfajul.

Megjegyzés. Megoldásunkból kiolvasható a következő, önmagában is érdekes állítás bizonyítása. Ha egy háromszögben az egyik csúcsot összekötjük a körülírt kör középpontjával, és a szemközti oldalt tükrözzük a hozzátartozó szögfelezőre, merőleges egyeneseket kapunk.

III. megoldás. Jelöljük az

A B M

háromszög köré írt körnek,

k_{1}

-nek és a háromszög

M

-beli külső szögfelezőjének,

t

-nek a ,,másik'' metszéspontját

N

-nel (vagyis

N

t

és

k_{1}

M

-től különböző metszéspontja minden olyan helyzetben, ha

t

metszi

k_{1}

-et, különben pedig

N

azonos

M

-mel). A kerületi szögekre vonatkozó tétel alapján

N

felezi a

k_{1}

-nek az

A B

ívét, és így

N

rajta van az

A B

szakasz felező merőlegesén,

A N = B N

. Tükrözzük az

A

B

O_{1}

pontokat

t

-re, és jelöljük a kapott pontokat

A'

-vel,

B'

-vel és

O'_{1}

-vel. A fentiek szerint

O_{1} M O'_{1} N

rombusz, és

N

A B B' A'

trapéz köré írható kör középpontja (4. ábra).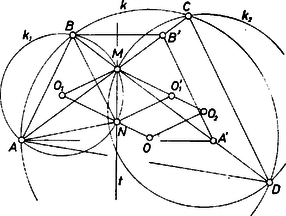

4. ábra

Mivel

A B C D

konvex húrnégyszög, az

M C D

és

M B' A'

, háromszögek megegyező körüljárásúak, és centrálisan hasonlóak. Emiatt

O_{2}

-t a

C D

szakasz

N O'_{1}

-vel párhuzamos felező merőlegese metszi ki

M O'_{1}

-ből és ugyanez a felező merőleges metszi ki

O_{1} N

-ből

O

-t. (Szemléletesen mondva: az

M

-centrumú nagyítás ‐ vagy kicsinyítés ‐ közben az

M O'_{1}

N O_{1}

,,síneken'' futnak az

O_{2}

O

pontok.) Tehát

O_{1} M O_{2} O

paralelogramma.

Egyszerűsítéssel Kollár János (Bpest., Piarista Gimn., II. o. t.) dolgozatából.