Feladat:	1407. matematika gyakorlat	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1973/október, 62 - 65. oldal		PDF  |  MathML
Témakör(ök):	Síkra vonatkozó tükrözés, Kocka, Négyzetek, Szabályos testek, Térelemek és részeik, Térgeometriai bizonyítások, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1972/február: 1407. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.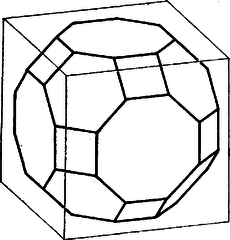   1. ábra   1. Legyen a kocka előlapja $ABCD=E$, testátlói $A{A}^{*}$, $B{B}^{*}$, $C{C}^{*}$, $D{D}^{*}$. Vegyünk fel $E$ belsejében egy $PQRSTUVZ=N$ szabályos nyolcszöget úgy, hogy középpontja essék egybe $E$-nek $E_0$ középpontjával, $PQ$ oldala párhuzamos és egyirányú legyen $BA$-val és közelebb legyen hozzá, mint a $TU$ oldal. Így $N$-nek mindegyik oldala párhuzamos $E$-nek valamelyik oldalával vagy átlójával (2. ábra). 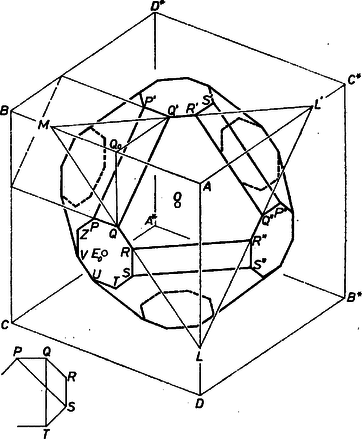    2. ábra   Tükrözzük alakzatunkat az $AB{A}^{*}{B}^{*}$ és az $AD{A}^{*}{D}^{*}$ átlós síkokra. A kocka mindkét esetben önmagába megy át, $N$ pedig az $AB{D}^{*}{C}^{*}=F$ fedőlap, illetve $AD{B}^{*}{C}^{*}=J$ jobb oldallapban fekvő, vele egybevágó $N\text{'}=P\text{'}Q\text{'}\text{...}Z\text{'}$, illetve $N\text{'}\text{'}=P\text{'}\text{'}Q\text{'}\text{'}\text{...}Z\text{'}\text{'}$ szabályos nyolcszögbe, és ezek öröklik az $E$ és $N$ közti kapcsolatokat, oldalaik párhuzamosak $F$, illetve $J$ valamelyik oldalával vagy átlójával és középpontjuk közös az illető lap középpontjával. Vegyük ezután az $N$-ből, $N\text{'}$-ből és $N\text{'}\text{'}$-ből álló alakzatnak a kocka $O$ középpontjára való (centrális) tükörképét, ezek rendre a kocka hátlapjának, alapjának, bal oldallapjának belsejében keletkeznek. Továbbá a kocka szimmetriái alapján $N$-nek és az 5 képnek a csúcsai rajta vannak az $O$ körüli $OQ$ sugarú gömbön, hiszen ez a kocka mindegyik lapját olyan körben metszi, melynek középpontja az illető lap középpontja, sugara pedig egyenlő $E_{0}Q$ hosszúságával, tehát köréje van írva az illető nyolcszögnek. Eddig nem használtuk ki $N$ oldalának hosszúságát, tehát az $N$-ből leszármaztatott pontokkal mint csúcsokkal meghatározott test köré mindig gömb írható, tekintet nélkül további lapjainak szabályos voltára. A tükrözés alapján $PQ$ egyenlő és párhuzamos $P\text{'}Q\text{'}$-vel, mert $PQ$ párhuzamos az itt használt tükörsík $BA$ egyenesével, így $P$, $Q$, $Q\text{'}$, $P\text{'}$ egy síkban vannak, a lap a kockából egyetlen síkmetszéssel kialakítható. Továbbá $QQ\text{'}$ merőleges a tükörsíkra és mivel $D{C}^{*}$ is merőleges rá, és az $AB$ élre is, azért $QQ\text{'}$ merőleges $PQ$-ra, $PQQ\text{'}P\text{'}$ téglalap. Ugyanezt a végeredményt kapjuk a kocka további 11 éle mentén is, ha a benne csatlakozó lapok két szabályos nyolcszögének az élhez közelebbi, vele párhuzamos oldalait állítjuk párba (pl. $R\text{'}S\text{'}$ párhuzamos $A{C}^{*}$-gal, mert ‐ amint $RS$ ‐ merőleges $AB$-re, és hasonlóan $Q\text{'}\text{'}P\text{'}\text{'}\parallel A{C}^{*}$, így $R\text{'}S\text{'}\parallel Q\text{'}\text{'}P\text{'}\text{'}$, és egyenlők $N$ oldalával. Egy síkban vannak a $Q$, $R$, $Q\text{'}$, $R\text{'}$, $Q\text{'}\text{'}$, $R\text{'}\text{'}$ pontok is. Ugyanis a $QR$ egyenesnek $AB$-vel, $AD$-vel való metszéspontját $M$-mel, illetve $L$-lel jelölve $AM=AL$, mert $QR$ párhuzamos a $BD$ átlóval, így az első két tükrözésben $L\text{'}$ és $M\text{'}\text{'}$ egybeesik, és $Q\text{'}$, $R\text{'}$ az $ML\text{'}$-n vannak, $R\text{'}\text{'}$, $Q\text{'}\text{'}$ pedig az $LL\text{'}$ egyenesen, a 6 csúcs az $MLL\text{'}$ síkon. Ez a 6 csúcs van $A$-hoz legközelebb az $N$-ből származtatott alakzat csúcsai közül; és további 6‐6 ilyen csúcs található a kocka további 7 csúcsának a környezetében is, az ezek által keletkezett hatszöglapok is egyetlen síkmetszéssel származtathatók a kockából. (A $PQQ\text{'}P\text{'}$ típusú négyszögeket és az utóbbi hatszögeket előállító metsző síkok egymást is metszik.) A $QRR\text{'}\text{'}Q\text{'}\text{'}R\text{'}Q\text{'}$ hatszög méreteiről is tehetünk megállapításokat. Szemben levő oldalai párhuzamosak, pl. $QQ\text{'}\parallel R\text{'}\text{'}Q\text{'}\text{'}$, mert $MLL\text{'}$ egyenlő oldalú háromszög, és $MQ\text{'}=MQ$, ugyanezért a hatszög mindegyik szöge ${120}^{\circ }$. Továbbá a hatszög minden második oldala $N$ oldalával egyenlő, és egyenlők az ezek közt levők is, pl. $QQ\text{'}=RR\text{'}\text{'}$, mert az eddigiek alapján $RL=MQ$, és $MQQ\text{'}$ és $LRR\text{'}\text{'}$ egybevágó egyenlő oldalú háromszögek. Ezek szerint a $PQ=QQ\text{'}$ egyenlőség biztosításával a mondott 12 téglalap és a 8 hatszög egy csapásra négyzetté, illetve szabályos hat hatszöggé specializálódik. Legyen a kocka éle $AB=a$ és $N$ oldala $PQ=b$, ekkor erre merőleges átlója a vele egyenlő $PS$ által létrehozott részekből $\begin{array}{c}{\displaystyle QT=b\left(1+\sqrt[]{2}\right)\mathrm{,}}\end{array}$ így $Q$-nak az $AB$-n levő $Q_0$ vetületétől való távolsága $\begin{array}{c}{\displaystyle Q{Q}_0=\frac{AD-QT}{2}=\frac{a}{2}-\frac{b\left(1+\sqrt[]{2}\right)}{2}\mathrm{,}}\end{array}$ a $QQ\text{'}{Q}_0$ egyenlő szárú derékszögű háromszög átfogójaként $\begin{array}{c}{\displaystyle QQ\text{'}=\sqrt[]{2}Q{Q}_0=\frac{a}{\sqrt[]{2}}-\frac{b\left(1+\sqrt[]{2}\right)}{\sqrt[]{2}}\mathrm{,}}\end{array}$ és így a mondott $PQ=QQ\text{'}$ követelményből $\begin{array}{c}{\displaystyle b=\frac{a}{7}\left(2\sqrt[]{2}-1\right)=a\cdot 0\mathrm{,}261.}\end{array}$ Ezek alapján a $PQQ\text{'}P\text{'}$ lap a $BC$ és $B{D}^{*}$ élekből, $Q{Q}_0=\frac{a}{14}\left(4-\sqrt[]{2}\right)=a\cdot 0\mathrm{,}184$ darabot metsz le, és párhuzamos $BA$-val; a $QRR\text{'}\text{'}Q\text{'}\text{'}R\text{'}Q\text{'}$ szabályos hatszöglapot lemetsző sík pedig az $A$-ból induló élekből ${\displaystyle \begin{array}{c}\hfill {\displaystyle AM=\frac{LM}{\sqrt[]{2}}=\frac{2MQ+b}{\sqrt[]{2}}=\sqrt[]{2}\cdot QQ\text{'}+\frac{b}{\sqrt[]{2}}=b\left(\sqrt[]{2}+\frac{1}{\sqrt[]{2}}\right)=\frac{3a}{14}\left(4-\sqrt[]{2}\right)=}\hfill \\ \hfill {\displaystyle =3\cdot Q{Q}_0=a\cdot 0\mathrm{,}552}\hfill \end{array}}$ darabot metsz le. 2. Hasonlóan látható be, hogy a test szabályos oktaéderből is leszármaztatható, ha kiindulunk az egyik lapjára rajzolt, vele koncentrikus olyan szabályos hatszögből, amelynek oldalai párhuzamosak a vett oktaéderlap éleivel, majd ezt tükrözzük a vele szomszédos lapokra a lapszög felezősíkján át, majd a test középpontjára, végül úgy választjuk a hatszög oldalát ‐ a test leendő élét ‐, hogy két hatszög egymáshoz legközelebbi oldalai egy négyzet két szemben fekvő oldalát adják (3. ábra). 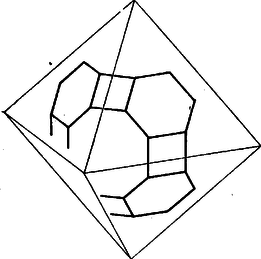    3. ábra   A szükséges számítások azonban a fentieknél bonyolultabbak, kevesebb a számítást könnyítő dérékszög. Beláthatjuk ezt abból is, hogy a 8 db szabályos hatszöglapot kellően meghosszabbítva szabályos oktaédert kapunk. Ebből könnyebb az új test éle és az oktaéder éle közti kapcsolat meghatározása.   Megjegyzések. 1. Hasonlóan a test négyzetlapjait kellően meghosszabbítva ún. rombdodekaédert kapunk,${}^{*}$ ebből is előállítható a test alkalmas síkmetszésekkel (4. ábra). 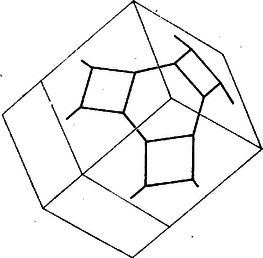    4. ábra   2. A vizsgált test egyike az ún. arkhimédészi félszabályos testeknek (minden lapjuk szabályos sokszög de nem mind egybevágók ‐ és minden csúcsának a "környezete'' mint triéder egybevágó egymással). ${}^{*}$Lásd: Csákány Béla: A méhek lépsejtjeiről, matematikus szemmel. K. M. L. 43 (1971) 109‐117. old., élesebben 113‐114. old.