Kezdőlap


Feladat:	1400. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Horváth Eszter , Horváth Gyöngyi , László Andrea , Németh József
Füzet:	1972/december, 214 - 217. oldal		PDF \| MathML
Témakör(ök):	Egyéb sokszögek hasonlósága, Forgatva nyújtás, Derékszögű háromszögek geometriája, Négyszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1972/január: 1400. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Tegyük fel, hogy a keresett $A B C D$ négyszög pozitív körüljárású (ez azt jelenti, hogy ha a csúcsokat az $A$ , $B$ , $C$ , $D$ sorrendben járjuk végig, eközben a téglalap középpontját az óramutató járásával ellentétes irányban kerüljük meg). Forgassuk el az $A$ körül a $B$ csúcsot pozitív irányban $90^{\circ}$ -kal, az $A D$ szakasz $B'$ pontját kapjuk, melyre $A B' = A B$ . Ha $A$ körül az egész $B C$ egyenest elforgatjuk pozitív irányban $90^{\circ}$ -kal, az $A D$ -re merőleges, $B'$ -n átmenő egyenest kapjuk. Ezen az egyenesen lesz az $M$ pont forgatottja is, az $M'$ pont. Az $A$ centrumú, $5 : 2$ arányú nagyítás $A B' : A D = A B : A D = 2 : 5$ miatt $B'$ -t $D$ -be viszi, tehát $M'$ -höz a $C D$ egyenes valamely $M_{1}$ pontját rendeli hozzá (1. ábra).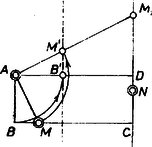

1. ábra

M'

és

M_{1}

pontokat adataink alapján könnyen megszerkeszthetjük : ha az

A M

-re merőleges,

A

-n átmenő egyenesre

A

-ból kiindulva alkalmas irányban felmérjük az

A M

szakasz felét kétszer,

M'

-t kapjuk (erre különben túl nagy szükségünk nincs), ha pedig ötször mérjük fel

A M

felét, akkor

M_{1}

et kapjuk (jelöljük

M_{2}

-vel azt a pontot, amit az ellentétes irányú felmérésből kapunk). Ekkor

A

merőleges vetülete az

M_{1} N

egyenesen

D

, az

M

-en átmenő,

A D

-vel párhuzamos egyenesen pedig

B

, végül

C

-t

B

-nek

M_{1} N

-re való vetítésével kapjuk. (Ha

M_{1}

helyett a közben megszerkesztett

M_{2}

-t használjuk, ugyanezzel az eljárással negatív körüljárású megoldást kapunk.) A kapott négyszög a szerkesztés szerint téglalap, és a

B C

oldal egyenese átmegy

M

-en, a

C D

oldal egyenese átmegy

N

-en. Ha a

C D

egyenest az

A

centrumból

2 : 5

arányban kicsinyítjük, az

M'

-n átmenő egyenest kapjuk, ezt

A

körül negatív irányban

90^{\circ}

-kal elforgatva

M

-en átmenő egyenest kapunk. Tehát

B

-t

D

-ből az

A

centrumú

2 : 5

arányú kicsinyítéssel, majd egy ezt követő, ugyancsak

A

centrumú

(- 90^{\circ})

-os forgatással kapjuk. Emiatt

A B C D

pozitív körüljárású, és benne

A B : B C = 2 : 5

. Hasonlóan látható be, hogy az

M_{2}

-ből kapott négyszög is megfelel a feladat követelményeinek, és negatív körüljárású.
Eddig úgy értelmeztük a feladat követelményeit, hogy a mondott oldalak egyenesei menjenek át az

M

és

N

pontokon. Így lesz ez még a következő lépésben is, amikor a megoldások számát határozzuk meg. Nyilván nincs megoldása a feladatnak, ha

M

vagy

N

azonos

A

-val (

M

és

N

viszont lehetnek azonosak). Szerkesztésünk első lépései, a forgatás és a nyújtás mindig végrehajthatóak. Előfordulhat, hogy

M_{1}

, vagy

M_{2}

azonos lesz

N

-nel. Ez nyilván csak úgy lehet, ha

A M

és

A N

merőlegesek egymásra, és

A M : A N = 2 : 5

. Ha ez így van, a feladatnak végtelen sok megoldása van, a

C D

egyenes tetszőleges, az

N

-en átmenő, de

A

-n át nem menő egyenes lehet.
Nem folytathatjuk a fent leírt úton szerkesztésünket akkor sem, ha az

M_{1} N

egyenes átmegy

A

-n (és akkor nyilván

M_{2} N

is átmegy), vagyis amikor

M A

merőleges

N A

-ra, de

M A : N A \neq 2 : 5

. Ebben az esetben a feladatnak nincs megoldása. Minden más esetben (ha tehát az

M A N

szög nem

90^{\circ}

-os) az

M_{1}

és

M_{2}

pontokból egy‐egy megoldást kapunk, tehát a feladatnak két megoldása van.
Érvényesek az eddigi állításaink akkor is, ha a feladat szövegét úgy értelmezzük, hogy az

M

és

N

pontoknak a

B C

és

C D

szakaszok belsejében kell lenniük, csak a kapott megoldások nem mind lesznek megfelelőek. Ha

M

valóban a

B C

N

C D

szakaszon van (és a négyszög körüljárása pozitív), akkor

M_{1}

C D

szakasz

D

-n túli meghosszabbítására kerül, tehát

N

-ből az

A M_{1}

szakasz hegyesszög alatt,

M M_{1}

pedig tompaszög alatt látszik. Így rögzített

A

M

pontok mellett

N

-nek az

A M_{1}

feletti

k_{1}

Thalész‐körön kívül, az

M M_{1}

feletti

g_{1}

Thalész‐körön pedig belül kell lennie (2. ábra).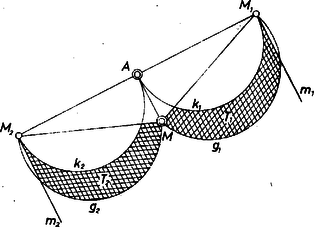

2. ábra

Mivel

M M_{1}

elválasztja az

A

N

pontokat, és az

A M_{1} N

szög hegyesszög,

N

-nek az

M M_{1}

egyenes

A

-t nem tartalmazó oldalán és az

A M_{1}

re merőleges,

M_{1}

-en átmenő

m_{1}

egyenesnek

A

-t tartalmazó oldalán kell lennie. Így kapjuk azt a

T_{1}

tartományt, ahol

N

-nek lennie kell, ha a négyszög pozitív körüljárású ; és negatív körüljárás esetén

T_{1}

-nek

A M

-re vonatkozó

T_{2}

tükörképe lesz

N

lehetséges helye.
Az olvasóra hagyjuk annak belátását, hogy ha

N

T_{1}

-ben vagy

T_{2}

-ben van, akkor valóban egy megoldást kapunk.

Horváth Eszter (Budapest, Ságvári E. Gyak. Gimn., II. o. t.)

II. Megoldás. Ismét olyan megoldást keresünk, amelyben a téglalap oldalegyenesei mennek át az

M

N

ponton. Az oldalak adott aránya alapján a keresetthez hasonló téglalapot szerkesztünk, ebben az átlónak a rövidebb oldallal bezárt

α

szöge megadja az

A C D ∢

nagyságát.

α

-val vagy

(180^{\circ} - α)

-val egyenlő az

A N

szakasznak

C

-ből vett látószöge aszerint, hogy

N

-en a

C D

félegyenes megy át vagy a

D C

oldal

C

-n túli meghosszabbítása. Eszerint

C

-nek rajta kell lennie az

A N

szakasz

α

és

180^{\circ} - α

nyílású látókörívpárjai valamelyikén ‐ vagyis a 3. ábra

k_{1}

és

k_{2}

köreinek egyikén (hiszen egy ilyen

α

szögű ív és az

A N

egyenes másik partján levő

(180^{\circ} - α)

szögű ív együtt egy teljes kört adnak).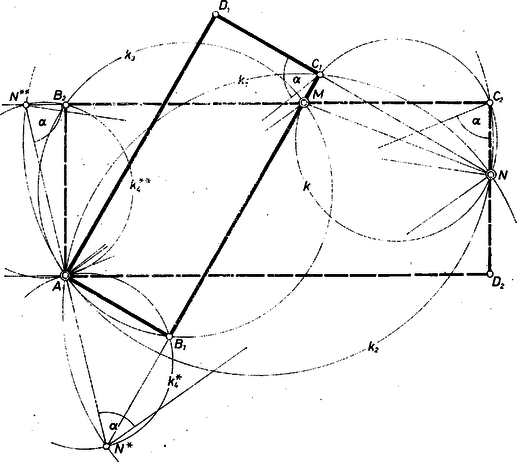

3. ábra

Másrészt

C

rajta van az

N M

szakasz mint átmérő fölötti

k

Thalész‐körön is.
Ezek alapján

C

csúcsként megfelel akár a

k_{1}

k

, akár a

k_{2}

k

körpár közös pontja, a keresett téglalap két oldalegyenese

C N

és

C M

, a másik kettő pedig ezekre merőleges és átmegy

A

-n.
A kapott téglalapban az

A C D

szög

α

-val egyenlő, ezért az

A B : B C

arány egyenlő a "minta‐téglalap'' oldalainak arányával, továbbá a

C

-ben összefutó oldalak átmennek

M

-en,

N

-en, tehát a szerkesztés helyes.

Mivel

N

mind a három körnek közös pontja, azért mindig van megoldása a feladatnak. (Ha

k

érinti pl.

k_{1}

-et, akkor

C

-ként maga

N

veendő. A 3. ábrán

k_{1}

-ből adódik az

A B_{1} C_{1} D_{1}

téglalap,

k_{2}

-ből az

A B_{2} C_{2} D_{2}

László Andrea (Székesfehérvár, Teleki Blanka Gimn., I. o. t)

Horváth Gyöngyi (Szeged, Radnóti M. Gimn., II. o. t.)

Megjegyzés. Az

α

látószöget célszerű mindjárt "helyben'' előállítani : az

A N

alap fölé mindkét oldalán

2 \cdot A N / 5

magasságú téglalapot (ill. csak

N A N^{*}

, ill

N A N^{* *}

derékszögű háromszöget) szerkeszteni, ezek körülírt köre

k_{1}

, ill

k_{2}

III. Megoldás. Vehetjük

B

-t vagy

D

-t is téglalapunk elsőként meghatározandó csúcsa szerepére, annak ellenére, hogy rájuk csak egy‐egy mértani helyet ismerünk : a

B

csúcs az

A M

szakasz fölötti

k_{3}

D

pedig az

A N

szakasz fölötti

k_{4}

Thalész‐körön van. Ugyanis minden megoldásban

B

D

-nek a képe abban az

A

centrumú elfordítva zsugorításos transzformációban, melynek arányszáma

2 : 5

és szöge

90^{\circ}

az egyik vagy a másik irányban. Ezért

B

-t a

k_{3}

-ból

k_{4}

-nek a mondott transzformációval adódó

k_{4}^{*}

, ill.

k_{4}^{* *}

képe metszi ki. (A 3. ábrán csak e transzformáltak láthatók, mint

A N

-nek

A N^{*}

A N^{* *}

képei fölötti Thalész‐körök.)

Megjegyzés. Így

A B_{1} N^{*} ∢ = A B_{1} M ∢ = 90^{\circ}

, tehát az első téglalap

B_{1} C_{1}

oldalegyenese azonos az

M N^{*}

egyenessel,

B_{2} C_{2}

pedig ugyanígy

M N^{* *}

-gal. Ezzel lényegében új megoldást kaptunk, itt kevesebb körre van szükségünk.

IV. Megoldás. Jelöljük

P

-vel az

M

-en átmenő,

A N

-re merőleges egyenesnek

A D

-vel való metszéspontját. Ez kijelölhető, ugyanis származtatásánál fogva az

M P

szakasz ugyanakkora szöggel hajlik

B A

-hoz, mint az

A N

szakasz a

B C

-hez,így a szakaszok aránya egyenlő a vetületek arányával :

\begin{matrix} M P_{i} : A N = B_{i} A : B_{i} C_{i} = 2 : 5, \\ M P_{i} = \frac{2}{5} A N, \end{matrix}

i = 1

, 2, hiszen ez a szakasz

M

-től mindkét irányban fölmérhető (4. ábra). Ezzel már készen is vagyunk.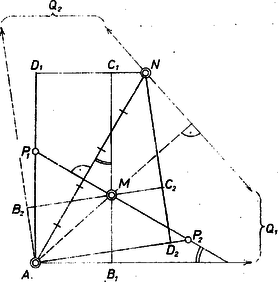

4. ábra

Ugyanezen elv szerint felhasználható lenne az

A B

egyenesnek az a

Q

pontja, ahol az

N

-ből

A M

-re állított merőleges áthalad.

Németh József (Eger, Gárdonyi G. Gimn., II. o. t.)