Kezdőlap


Feladat:	1399. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Beck L. , Borbély A. , Boros P. , Éltető L. , Fazekas László , Fördős J. A. , Gáspár Gy. , Horváth Eszter , Jakab T. , Kelemen G. , Molnár György , Pesti G. , Raikovich P. , Simonyi B. , Smohay T. , Szabó Zs. , Szalay P. , Szöllős L. , Torma T. , Vladár K. , Zahalka G.
Füzet:	1972/szeptember, 18 - 19. oldal		PDF \| MathML
Témakör(ök):	Eltolás, Magasságvonal, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1972/január: 1399. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Ismeretes, hogy hegyesszögű háromszögben a talpponti háromszög belső szögfelezői rendre azonosak az eredeti háromszög magasságvonalával. (Ez következik például abból, hogy a háromszög magasságpontját $M$ -mel jelölve,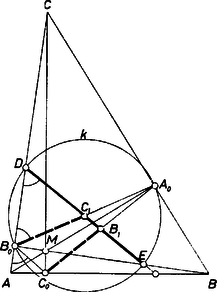

\begin{matrix} A B_{0} C_{0} ∢ = A M C_{0} ∢ = A_{0} M C ∢ = A_{0} B_{0} C ∢, \end{matrix}

mert a középső két szöget ugyanaz a két egyenes határozza meg, az első és utolsó egyenlőség pedig abból következik, hogy az

A M,

illetve

C M

szakasz a

B_{0}

C_{0}

, illetve

A_{0}

B_{0}

pontokból derékszög alatt látszik, tehát

A_{0}

B_{0}

M

C_{0}

, illetve

A_{0}

C

B_{0}

M

egy-egy körön vannak.)

Rajzoljuk meg az

A_{0} B_{0}

szakasz feletti

k

Thalész-kört (középpontja

C_{1}

). A

C

pont ebben nincs benne, mert

C

-ből

A_{0} B_{0}

hegyesszög alatt látszik. Emiatt

k

metszi a

B_{0} C

szakaszt, jelöljük a metszéspontot

D

-vel. Így a

B_{0} C_{1} D

háromszögben

B_{0} C_{1} = D C_{1}

és a

C_{1} D B_{0}

és

D B_{0} C_{1}

szögek egyenlők. Az utóbbi viszont ‐ mint láttuk ‐ egyenlő a

C_{0} B_{0} A

szöggel. Egyező ezeknek a szögeknek a forgási iránya is (az ábrán mindegyiké megegyezik az óramutató járásával), tehát

C_{1} D

párhuzamos

B_{0} C_{0}

-lal, és így átmegy

B_{1}

-en.
Ezzel tulajdonképpen azt láttuk be, hogy a

B_{1} C_{1}

egyenest a

C_{1}

-túl épp az

A_{0} B_{0}

szakasz felével kell meghosszabbítani, hogy az

A B C

háromszög határára ‐ jelen esetben az

A C

szakaszra ‐ érjünk.
Eddigi meggondolásainkat elmondhatjuk betűk nélkül is: azt kaptuk, hogy egy hegyesszögű háromszög talpponti háromszögének bármelyik középvonalát a talpponti háromszög bármelyik felezett oldalán túl épp az illető oldal felével kell megtoldani, hogy az eredeti háromszög határára jussunk. Ha tehát egy középvonalat mindkét irányban megtoldunk, akkor a teljes szakasznak a részei ‐ azaz a középvonal egyeneséből az eredeti háromszögbe eső darabnak a részei ‐ rendre egyenlők a talpponti háromszög egy-egy oldalának a felével, és a teljes szakasz hossza egyenlő a talpponti háromszög félkerületével. Ezzel a feladat állításának a bizonyításán túl azt is meghatároztuk, mekkorák a szóban forgó szakaszok.
2. Rátérünk a feladat kérdésének a vizsgálatára. Jelöljük egy tetszőleges tompaszögű háromszög tompaszögénél levő csúcsát,

M

-mel, a másik két csúcsot

A

-val és

B

-vel, a háromszög magasságpontját

C

-vel. Ekkor az

A B C

háromszög hegyesszögű, és a talpponti háromszöge azonos

A B M

talpponti háromszögével. Jelöljük ennek a csúcsait továbbra is

A_{0}

-lal,

B_{0}

-lal,

C_{0}

-lal, az

A_{0} B_{0} C_{0}

háromszög oldalfelező pontjait rendre

A_{1}

-gyel,

B_{1}

-gyel,

C_{1}

-gyel, az

A_{0} B_{0}

feletti Thalész-kört

k

-val.
Mivel az

A_{0} B_{0}

szakasz

M

-ből tompaszög alatt,

B

-ből pedig hegyesszög alatt látszik, azért

M

k

belsejében,

B

pedig a

k

-n kívül van, tehát

k

metszi a

B M

szakaszt, jelöljük a metszéspontot

E

-vel. Ez a már használt

D

-vel szemközti pontja

k

-nak, mert

B_{0} B ⊥ B_{0} C

, emiatt

E

is rajta van a

B_{1} C_{1}

egyenesen. Ha tehát egy hegyesszögű háromszög talpponti háromszögének a középvonalára visszafelé mérjük fel az oldal felét, az eredeti háromszög magasságvonalára jutunk. (Ez így egy kicsit pontatlan: hogy melyik magasságvonalra, az abból határozható meg, hogy a választott középvonal, a felmért oldal és a magasságvonal az eredeti háromszög különböző csúcsaihoz tartozik.)
Ezek szerint a

C_{1} B_{1}

félegyenesre az

A_{0} B_{0}

oldal felét mérve a

B B_{0}

magasságvonalra jutunk, a

B_{1}

-en túli meghosszabbításra pedig az

A_{0} C_{0}

felét mérve az

A B

oldalra jutunk, tehát a

B_{1} C_{1}

egyenesnek az

A B M

háromszögbe eső szakasza egyenlő

\frac{1}{2} (A_{0} C_{0} + C_{0} B_{0} - B_{0} A_{0})

-lal. Hasonlóan látható, hogy ennyivel egyenlők az

A_{1} B_{1}

A_{1} C_{1}

egyenesek

A B M

-beli szakaszai is, tehát a feladat eredeti állítása tompaszögű háromszögre változtatás nélkül igaz, csak az általunk a szakaszok közös értékéről adott kiegészítést kell módosítani.