Kezdőlap


Feladat:	1395. matematika gyakorlat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Kelemen Dezső
Füzet:	1973/január, 22 - 23. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Paraméteres egyenletek, Gyökök és együtthatók közötti összefüggések, Derékszögű háromszögek geometriája, Hossz, kerület, Téglalapok, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1971/december: 1395. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Legyen az $A B C D$ téglalapban $A B = a$ , $B C = k a$ , a két levágott háromszög $A A_{1} A_{2}$ és $C C_{1} C_{2}$ úgy, hogy $A_{1} A_{2} = A_{2} B = B C_{1} = C_{1} C_{2} =$ $= C_{2} D = D A_{1} = x$ . Így $A A_{1} = A D - D A_{1} = C C_{1} = k a - x$ , és $A A_{2} = C C_{2} =$ $= a - x$ , ezért a derékszögű háromszögekből:

\begin{matrix} A A_{1}^{2} + A A_{2}^{2} - A_{1} A_{2}^{2} = {(k a - x)}^{2} + {(a - x)}^{2} - x^{2} = \\ = x^{2} - 2 (1 + k) a x + (1 + k^{2}) a^{2} = 0. \end{matrix}

A gyökök valósak és különbözők, mert a diszkrimináns pozitív:

8 a^{2} k > 0

, és mindkettő pozitív, mert összegük is, szorzatuk is pozitív. A két gyök összege

2 a (1 + k)

, egyenlő a téglalap kerületével, ezért csak a kisebb gyök felelhet meg. S mivel ez a feladat közlése szerint meg is felel, azért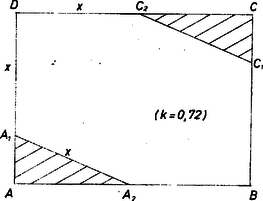

\begin{matrix} x = a (1 + k - \sqrt[]{2 k}) < k a, \\ 1 - \sqrt[]{2 k} < 0, k > \frac{1}{2} . \end{matrix}

Ezt mondhatjuk

k

értékéről.
2. A kérdéses arány

\begin{matrix} q = \frac{6 x}{2 (1 + k) a} = \frac{3 (1 + k - \sqrt[]{2 k})}{1 + k} = 3 - \frac{3 \sqrt[]{2 k}}{1 + k}, \end{matrix}

(1)

ennélfogva ha

0 < k_{1} < k_{2} \leq 1

, akkor a megfelelő arányértékek különbsége

\begin{matrix} q_{2} - q_{1} = (3 - \frac{3 \sqrt[]{2 k_{2}}}{1 + k_{2}}) - (3 - \frac{3 \sqrt[]{2 k_{1}}}{1 + k_{1}}) = 3 \sqrt[]{2} (\frac{\sqrt[]{k_{1}}}{1 + k_{1}} - \frac{\sqrt[]{k_{2}}}{1 + k_{2}}) = \\ = 3 \sqrt[]{2} \frac{(\sqrt[]{k_{1}} - \sqrt[]{k_{2}}) (1 - \sqrt[]{k_{1} k_{2}})}{(1 + k_{1}) (1 + k_{2})} < 0, tehát \\ q_{2} < q_{1}, \end{matrix}

ugyanis a számláló első tényezője negatív, hiszen a föltevés szerint

\sqrt[]{k_{1}} < \sqrt[]{k_{2}}

, a többi tényező pozitív, mert

0 < k_{1} k_{2} < 1

.
Kimondhatjuk tehát, hogy az arány az (1) képlet szerint függ

k

-tól és

k

növekedésével monoton csökken.

Kelemen Dezső (Kaposvár, Táncsics M. Gimn., II. o. t.)