Feladat: 1392. matematika gyakorlat Korcsoport: 14-15 Nehézségi fok: -
Megoldó(k):  Pócsi György 
Füzet: 1972/november, 147 - 149. oldal  PDF  |  MathML 
Témakör(ök): Bűvös-négyzetek, Logikai feladatok, "a" alapú számrendszer (a >1, egész szám), Gyakorlat
Hivatkozás(ok):Feladatok: 1971/december: 1392. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.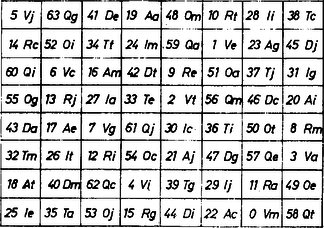

 
1. ábra
 
 
2. ábra
 

a) Bűvös négyzeten n2 számnak n sorba és egyúttal n oszlopba való olyan elrendezését szokás érteni, melyben a számok összege mindegyik sorban, mindegyik oszlopban és mind a két átló mentén ugyanannyi. A legismertebb bűvös négyzetekben az egymás utáni 1, 2, 3, ..., n2 számokat szokás elrendezni, itt viszont n=8 esetére a 0, 1, ..., 63 számok szerepelnek, a feladat második része pedig egészen más összefüggésű számegyüttesből alakuló bűvös négyzetet sejtet.
b) Az első fiú ‐ úgy látszik ‐ ennek a 8+8+2=18 db 8-tagú összeadásnak az elvégzését, ellenőrzését vette tervbe, először az eredeti elrendezésben, majd pedig azon, amelyiken a 0,1,2,...,63 számokat rendre a négyzetükkel: 0-val, 1-gyel, 4-gyel, ..., 3969-cel fogja pótolni.
A második fiú helyesen fölismerte, hogy minden egyes szám mellett a betűpár az illető szám nyolcas számrendszerbeli alakjának ,,titkos'', ,,rejtjelezett'' megismétlése: ha az első helyen álló
V, R, A, I, T, D, O, Q
nagybetűk helyére, egyszersmind a második helyen álló
m, e, t, a, i, j, c, g
kisbetűk helyére rendre a
0,1,2,3,3,4,5,6,7
számjegyet írjuk, megkapjuk a szám nyolcas számrendszerbeli alakját, pl. az első sorban, majd az utolsóban
Vj=8)05=5,Qg=8)77=7⋅8+7=63,Vm=00=0.

Ezek szerint átírva az 1. ábrát a nyolcas rendszerbe, a 2. ábrát kapjuk.
Észrevette továbbá, hogy minden egyes betűfajta az ábrán 8-szor fordul elő, éspedig úgy elrendezve, hogy mindegyik betű mind a 8 sorban, mind a 8 oszlopban és mind a 2 átlóban pontosan egyszer lép föl. (Az A nagybetű és az a kisbetű egyező kiejtésének viszont nincs jelentősége, ugyanígy az I, i és a T, t párnak sincs.) Ez az észrevétel fölöslegessé teszi az alapelrendezés soraiban, oszlopaiban és átlóiban az összeg ellenőrzését, enélkül is tudjuk, hogy mind a 18 vonalon ‐ a sorrendtől, ami itt lényegtelen, eltekintve ‐
(0+1+2+...+7)⋅8+(0+1+2+...+7)=28⋅9(=252)
a számok összege, tehát az elrendezés valóban nyolcadrendű bűvös négyzet. (Itt mutatkozik meg annak az előnye, hogy nem 1-től 64-ig használták fel a természetes számokat; ugyanis csak a 0-tól 63-ig terjedő számok nyolcas rendszerbeli, mindenütt kétjegyű felírásában van meg minden számjegynek az ugyanannyiszor való előfordulása; már 64=8)100 lenne.)
c) Előnyös a számok 8-as rendszerbeli alakjának használata akkor is, ha helyükre a négyzetüket írjuk be, az x, y jegyekkel írt szám helyére ezt;
8)xy2¯=(8x+y)2=64x2+16xy+y2.
Eszerint mind a 18 vonalösszegben egyformán föllép az első és harmadik tag címén (02+12+...+72)(64+1), elég tehát azt vizsgálni, egyenlő-e a 16xy alakú második tagok összege mindenütt, illetve egyszerűbben az xy tagoké, azaz ha a 2. ábra minden egyes száma helyére jegyeinek a szorzatát írjuk.
További észrevételek ezt a vizsgálatot is egyszerűsítik.
 

α) A 2. ábrának a középpontjára nézve szimmetrikus mezőiben álló 2‐2 szám összege mindig 8)77. Ezt a tulajdonságot is jegyekre felbontva célszerű ellenőrizni, példákat mutat rá a 3a és 3b ábra, amelyeken kiemeltük a nyolcas értékű helyeken álló 1 és 6 jegyeket, ill. az 1-es értékű helyeken álló 0 és 7 jegyeket, így jól látszik a centrális szimmetria, az ilyen számpárok összegében mindkét helyen 7 áll.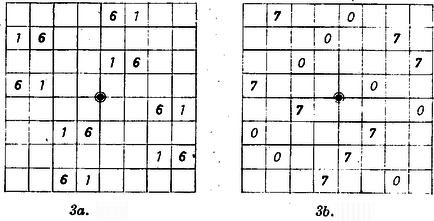
 
 
3a. ábra         3b. ábra
 

Eszerint az 8)xy szám tükrös helyzetű párjában a szorzat (7-x)⋅(7-y)=49-7(x+y)+xy, és ha a számjegypárokból képzett 8 szorzat összege egy sorban vagy oszlopban S, akkor a centrálisan szimmetrikus sorban, oszlopban
S'=8⋅49-(7+7)(0+1+2+...+7)+S=S,
hiszen x és y szerepében a 8 tag egyformán a 0, 1, ..., 7 jegyeket tartalmazza.
Eszerint az egymás utáni sorok, oszlopok (hasábok) számjegyszorzatainak összegét s1-gyel, s2-vel, ..., s8-cal, ill. h1-gyel, h2-vel, ..., h8-cal jelölve si=s9-i és hi=h9-i (i=1,2,3,4).
β) Az egyik átló mindegyik számában a jegyeket fölcserélve, vagyis xy¯-hoz képezve yx¯-et, a másik átló számait kapjuk, tehát a számjegyszorzatok összege a két átlón egyenlő. (Egyik átlón sem találunk két egyenlő jeggyel írt, xx¯ alakú számot.)
γ) Hasonlóan: bármelyik sor mindegyik xy¯ számához megkeresve yx¯-et, ezek valamennyien ugyanabban az oszlopban állnak, a sor és oszlop közös mezején álló szám két jegye egyenlő, tehát az így párba állított soron és oszlopon a szorzatok páronként egyenlők. E sor- és oszloppárok ‐ közös számuk: 00, 11 ..., 77 sorrendjében ‐ :
s8=h7,s3=h5,s7=h1,s4=h3,s5=h6,s2=h8,s6=h4,s1=h2.


Ezt az α) alatt talált egyenlőségekkel egybevetve a 16 összeg 4 négytagú ,,értékközösségbe'' rendeződik:
s1=h2=h7=s8,s2=h8=h1=s7,s3=h5=h4=s6,s4=h3=h6=s5,


és így elég ezt ellenőriznünk: egyenlő-e a számjegyszorzatok összege az első négy sorban és a jobbra lejtő átlóban.
Mind az 5 kijelölt vonalon 98 ez az összeg, ebből látjuk, hogy valóban akkor is bűvös négyzet keletkezik, ha az 1. és 2. ábra számai helyére (a megfelelő tízes, ill. nyolcas rendszerben értve őket) a négyzetüket írjuk.
 

Pócsi György (Debrecen, Fazekas M. Gimn., II. o. t.)