Kezdőlap


Feladat:	1388. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Kiss Emil
Füzet:	1973/szeptember, 12 - 15. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Középpontos és egyéb hasonlósági transzformációk, Vetítések, Egyenlő szárú háromszögek geometriája, Trapézok, Projektív geometria, Párhuzamos szelők tétele, Párhuzamos szelők tételének megfordítása, Gyakorlat
Hivatkozás(ok):	Feladatok: 1971/november: 1388. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. Bebizonyítjuk a következő segédtételt: A tetszőleges $T_{1} T_{2} T_{3} T_{4}$ négyszög $T_{2} T_{3}$ és $T_{4} T_{1}$ oldalegyenesei messék egymást egy $U$ pontban, $T_{1} T_{3}$ és $T_{2} T_{4}$ átlói egy $U'$ -ben, így $T_{3} T_{4}$ akkor és csak akkor párhuzamos $T_{1} T_{2}$ -vel, ha az $U U'$ egyenes felezi a 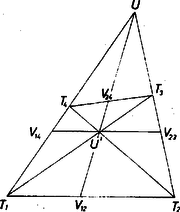$T_{1} T_{2}$ oldalt.
Húzzunk párhuzamost $U'$ -n át a $T_{1} T_{2}$ oldallal, jelöljük a $T_{1} T_{4}$ és a $T_{2} T_{3}$ oldallal való metszéspontját $V_{14}$ -gyel, ill. $V_{23}$ -mal, az $U U'$ egyenesnek a $T_{1} T_{2}$ és a $T_{3} T_{4}$ oldallal való metszéspontját $V_{12}$ -vel, ill. $V_{34}$ -gyel (1. ábra).

1. ábra

Ekkor az

U

T_{4}

T_{3}

csúcsú szögek szárait átmetsző párhuzamosok alapján mindenesetre

\begin{matrix} \frac{U' V_{14}}{V_{12} T_{1}} = \frac{U' U}{V_{12} U} = \frac{U' V_{23}}{V_{12} T_{2}}, & (1) \\ \frac{T_{2} T_{1}}{U' V_{14}} = \frac{T_{1} T_{4}}{V_{14} T_{4}}, & (2) \\ \frac{T_{1} T_{2}}{U' V_{23}} = \frac{T_{2} T_{3}}{V_{23} T_{3}} . & (3) \end{matrix}

Ha most még

T_{1} T_{2} | | T_{3} T_{4}

is fennáll, akkor (2) és (3) jobb oldalai egyenlők, ezért a bal oldalak nevezői is egyenlők:

U' V_{14} = U' V_{23}

, így az (1)-beli szélső törtek nevezői is egyenlők,

V_{12}

felezi

T_{1} T_{2}

-t, ami állításunk első része (és ekkor persze

V_{34}

is felezi

T_{3} T_{2}

-et,

U'

felezi

V_{14} V_{23}

-at).
Ha viszont, a

V_{12} T_{1} = V_{12} T_{2}

egyenlőséget tesszük föl, akkor az (1)-beli első és utolsó számláló is egyenlő, ezért (2) és (3) bal oldalai is egyenlők, ezért jobb oldalaik egyenlőségét fölhasználva

\begin{matrix} \frac{T_{2} T_{4}}{U' T_{4}} = \frac{T_{1} T_{4}}{V_{14} T_{4}} = \frac{T_{2} T_{3}}{V_{23} T_{3}} = \frac{T_{1} T_{3}}{U' T_{3}}, \end{matrix}

a szélső arányokból 1-et ‐ 1-et levonva

\begin{matrix} \frac{T_{2} U'}{U' T_{4}} = \frac{T_{1} U'}{U' T_{3}}, \end{matrix}

tehát

T_{1} T_{2} | | T_{3} T_{4}

; ezzel segédtételünk második részét is bebizonyítottuk.
2. Jelölje feladatunkban

E

és

G

S O

egyenesnek rendre az

A B

-n,

C D

-n levő pontját,

F

és

H

A B

-vel

O

-n át húzott párhuzamosnak rendre az

A D

-n,

B C

-n levő pontját, jelöljük továbbá az

E H

F G

egyenespár metszéspontját

J

-vel, az

E F

G H

párét

K

-val. Ekkor segédtételünk első része szerint

E

felezi

A B

-t, továbbá

O

F H

-t,

G

C D

-t felezi, hiszen föltevés szerint

A B | | C D | | F H

. Így pedig segédtételünk második részét az

F H J K

négyszögre alkalmazva

K J | | F H | | A B

, hiszen e négyszögben a két átló metszéspontja

G

, a

K F

J H

oldalegyenespáré

E

, az

E G

egyenes

O

-ban felezi az

F H

oldalt.
Ezek szerint ha

A B | | C D

és az

S

pont létrejön (vagyis

A B \neq C D

), akkor a kérdéses egyenes mindig párhuzamos

A B

-vet.

Kiss Emil (Budapest, Fazekas M. Gyak. Gimn., II. o. t.)

Megjegyzések. 1. Ha segédtételünknek csak az első felét bizonyítjuk (,,ha

A B | | C D

, akkor

E A = E B

G D = G C

és

D F = O H

''), akkor megoldásunkat így fejezhetjük be. Messe a

C D

egyenes

E H

-t

L

-ben,

E F

-et

M

-ben, ekkor

G L = G M

, és

\begin{matrix} \frac{F J}{G J} = \frac{F H}{G J} = \frac{H F}{G M} = \frac{H K}{G K}, \frac{F J}{G J} - 1 = \frac{F G}{G J} = \frac{H G}{G K}, \end{matrix}

G F H

és

G J K

háromszögek középpontosan hasonlók, tehát

J K | | F H | | A B

. (Tehát lényegében itt bizonyítjuk segédtételünk második részét.)
2. Többek ismert tételként hivatkoztak a segédtétel első részére. A korábbi tankönyvben valóban szerepelt ez, de a jelenlegiben nem. (Emiatt adtuk bizonyítását már az 1244. gyakorlatban is, K. M. L. 39 (1969) 62. oldal.) Egyébként az

A B = 2 \cdot D C

esetben

O

A B S

háromszög súlypontja és

S O

A B

-hez tartozó súlyvonal.
A segédtételt szemléletesen, így is kimondhatjuk: ha

A B | | C D

és

A B \neq C D

, akkor az

A B C D

trapéz ferdén szimmetrikus a szárak

S

metszéspontját az átlók

O

metszéspontjával összekötő egyenesre,

2

megfelelő pont összekötő egyenese párhuzamos

A B

-vel, és a köztük levő szakaszt az

S O

egyenes felezi.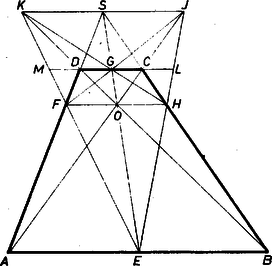

2. ábra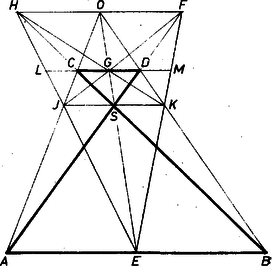

3. ábra

3. Bizonyításunkban a trapéz szárai és átlói nem játszottak egymástól lényegesen különböző szerepet. A bizonyítás érvényes a 3. ábrára is ‐ amelynek kiindulása a 2. ábráétól csupán a

C

és

D

fölcserélésében különbözik (vagyis itt

A B C D

hurkolt trapéz). Könnyen adódik az összehasonlításból az a sejtés, hogy a

J K

- szakasz felezőpontja éppen

S

, és hogy

J

K

rajta van az

A C

, ill.

B D

átlón; ezek bizonyítását ajánljuk az olvasónak.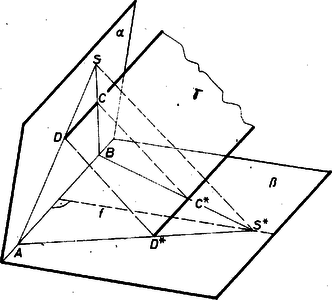

II. megoldás. Ha

A B C D

szimmetrikus trapéz, akkor az

S O

egyenes éppen a szimmetriatengely, merőleges az alapokra, az alakzatot előállító pontok egyenesek, is tükrös párokba kapcsolhatók, és így a kérdéses egyenes önmagának a képe, merőleges

O S

-re, párhuzamos az alappal. Eszerint tüstént készen vagyunk tennivalónkkal, ha találunk olyan transzformációt, amely bármely

A B C D

trapézt szimmetrikus trapézba visz át (és a további szerkesztő lépéseket meghagyja).

4. ábra

Vegyünk evégett az

A B

egyenesen át egy, az alakzatunk

α

síkjától különböző

β

síkot és benne az

A B

szakasz felező merőlegesén egy

S^{*}

pontot ‐ amely nincs rajta magán az

A B

szakaszon is ‐ és vetítsük rá alakzatunkat

β

-ra az

S S^{*}

-gal párhuzamos vetítő egyenesek felhasználásával. Mivel így az

A B S

háromszög képe az

A B S^{*}

egyenlő szárú háromszög, elég azt belátnunk, hogy a

C D

egyenes

C^{*} D^{*}

képe párhuzamos

A B

-vel. Valóban, a

C C^{*}

D D^{*}

párhuzamos vetítő egyenesek gamma síkja

α

-t

C D

-ben,

β

-t

C^{*} D^{*}

-ban metszi, és ha

A B

-nek és

C^{*} D^{*}

-nak volna egy közös

X

pontja, ez

α

β

γ

mindegyikében benne volna, tehát

A B

-nek és

C D

-nek közös pontja lenne, amit kizártunk. Így pedig a

C^{*} D^{*}

egyenes az

A B S^{*}

egyenlő szárú háromszögből szimmetrikus trapézt metsz le. Most már

J^{*} K^{*} | | A B

J^{*} K^{*}

visszavetítése

α

-ra a

J K

egyenes, és ez ugyanúgy párhuzamos

A B

-vel, amint azt

C^{*} D^{*}

-ról láttuk. Ezzel az állítást bebizonyítottuk.
(Három egyező ‐ tehát nem versenyszerű ‐ dolgozat ötlete alapján; egyébként kidolgozásuk egyformán hibás is.)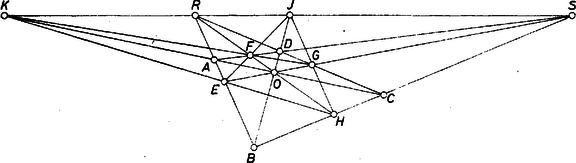

5. ábra

Megjegyzés. Ha

A

B

C

D

négy pont, semelyik három sincs egy egyenesen, az

A C

és

B D

, az

A D

és

B C

, az

A B

és

C D

egyenespár metszéspontja rendre

O

S

, ill.

R

, az

O S

egyenes közös pontja

A B

-vel és

C D

-vel

E

, ill.

G

, az

O R

egyenesé

A D

-vel,

B C

-vel

F

, ill.

H

, akkor az

E F

G H

és az

E H

F G

egyenespárok

J

K

metszéspontjai által meghatározott egyenes azonos az

R S

egyenessel (5. ábra). Ezt az állítást az ún. projektív geometriában egyszerűen bizonyítják. Az ábra mindegyik egyenesén a megbetűzött

4

pont ún. harmonikus pontnégyest alkot, az általuk meghatározott szakaszok közül kettő-kettőnek az aránya egyenlő, pl.

A E : B E = A R : B R

(és így persze

A E : A R = B E : B R

). Az érdeklődőknek ajánljuk Vigassy Lajos következő Középiskolai Szakköri Füzeteit: Geometriai transzformációk; Projektív geometria.