Kezdőlap


Feladat:	1381. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Füzet:	1972/május, 205 - 206. oldal		PDF \| MathML
Témakör(ök):	Magasságvonal, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1971/október: 1381. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A $B_{1}$ , $C_{2}$ pontok rajta vannak a keresett háromszögnek az $A B$ oldallal párhuzamos $c_{1}$ középvonalán, tehát a $B_{1} C_{2}$ egyenesre $C_{2}$ -ben állított merőleges a háromszögnek a $C$ csúcsból induló $m_{c}$ magasságegyenese. Ezen lesz rajta $C$ és a magasságnak az $A B$ oldalegyenesen levő $C_{0}$ talppontja (1. ábra).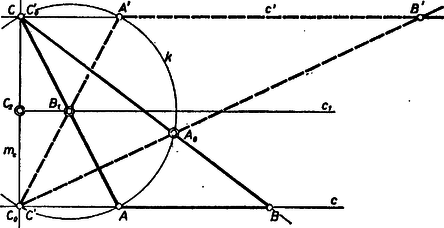

A_{0}

talppont rajta van az

A C

oldal mint átmérő fölé írt

k

Thalész-körön, melynek középpontja

B_{1}

. Ebből

k

megrajzolható, rajta lesznek az

A

C

csúcsok és a már mondott

C_{0}

talppont.
Mármost

m_{c}

és

k

két metszéspontjának egyikét

C

, másikát

C_{0}

szerepére megválasztva,

C

-nek

B_{1}

-re való tükörképe lesz

A

, a

B

csúcsot pedig az

A C_{0}

és

C A_{0}

egyenesek metszéspontja adja meg.
Bebizonyítjuk, hogy az

A B C

háromszög megfelel a követelményeknek. A tükrözés alapján

B_{1}

felezi

A C

-t; továbbá Thalész tétele szerint

A A_{0} ⊥ B C

(és

A_{0}

rajta van

B C

-n); ugyanezért

A B ⊥ C C_{0}

, másrészt

B_{1} C_{2}

merőleges

k

-nak

C C_{0}

húrjára, tehát

C_{2}

felezi

C C_{0}

-t.
Szerkesztő lépéseink egyértelműek,

C

és

C_{0}

szerepének megválasztása viszont kétféleképpen lehetséges, így általában

2

megoldása van a feladatnak (az 1. ábrán

C

C_{0}

-ból

A

és

B

, a fölcserélt

C'_{0}

és

C'

-ből

A'

és

B'

).
Ha azonban

C_{2}

egybeesik

B_{1}

-gyel ‐ ami azt jelenti, hogy a

C C_{0}

magasság azonos a

C A

oldallal és

C_{0}

azonos

A

-val, tehát a

C A B

szögnek

90^{\circ}

-nak kell lennie ‐, akkor a

c_{1}

és

m_{c}

egyenesek iránya nincs meghatározva, de

m_{c}

mindenesetre átmérője

k

-nak; így

C

k

-n tetszés szerint választható, a továbbiakban

B

meghatározásához

A C_{0}

egyenesként az

A

-ban

C A

-ra állított merőleges veendő. Ebben az esetben végtelen sok megoldás van; csak

A_{0}

és

k

-nak vele átellenes

A_{0}^{*}

pontja nem választható

C

szerepére, mert

C \equiv A_{0}

esetén

A B

is,

C B

is merőleges lenne

A C

-re, ill.

C \equiv A_{0}^{*}

esetén

A

azonos lenne

A_{0}

-lal, ami valódi háromszögben lehetetlen.
Az

m_{c}

egyenes akkor és csak akkor metszi

k

-t

2

egymástól különböző pontban, ha

B_{1} A_{0} > B_{1} C_{2}

, ez tehát szükséges feltétele a megoldhatóságnak. (

B_{1} A_{0} = B_{1} C_{2}

esetén

m_{c}

-nek és

k

-nak csak egy közös pontja van, ami nem lehetne egyszerre

C

is,

C_{0}

is.)

B_{1} A_{0} ≦ B_{1} C_{2}

esetén nincs megoldás. Ebből az is következik, hogy az

A_{0}

pont sem

B_{1}

-gyel, sem

C_{2}

-vel nem eshet egybe. (Előfordulhat az a különlegesség, hogy

k

és

m_{c}

egyik metszéspontja éppen maga az

A_{0}

pont, ilyen esetben persze

A_{0} C_{2} B_{1} ∢ = 90^{\circ}

. Ez nem teszi érvénytelenné a fent mondottakat,

A_{0}

alkalmas mind a

C

csúcs, mind a

C_{0}

talppont szerepére; mindkét esetben derékszögű háromszöget kapunk, a derékszög csúcsa

C

, ill.

B

.)
Végül a

B

-t meghatározó

A C_{0}

és

C A_{0}

egyenesek csak akkor nem metszik egymást, ha az

A_{0} C C_{0} A

húrnégyszög téglalap,

m_{c}

k

-t az

A_{0}

-lal átellenes

A_{0}^{*}

pontjában metszi (ami már az megindulási helyzetben felismerhető, abból hogy az

A_{0}

-ból

B_{1} C_{2}

-re bocsátott merőleges átmegy

C_{2}

-nek

B_{1}

-re vonatkozó tükörképén). Ilyen tulajdonságú

A_{0}

B_{1}

C_{2}

adott ponthármas esetében ismét nincs megoldás.
Megjegyezzük végül, hogy az

A B C

háromszög egybevágó lehet

A' B' C'

-vel, ha

A_{0}

rajta van a

B_{1} C_{2}

egyenesen, ekkor egymás tükörképei

B_{1} C_{2}

-re. Azonban ekkor is külön megoldásnak számít mindegyik, mert ha helyzetadatokból indulunk ki, akkor két különböző helyzetűmegoldás különbözőnek tekintendő.