Feladat: 1377. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: nehéz
Füzet: 1973/április, 152 - 154. oldal  PDF  |  MathML 
Témakör(ök): Síkra vonatkozó tükrözés, Vetítések, Négyszög alapú gúlák, Egyenlő szárú háromszögek geometriája, Hossz, kerület, Négyzetek, Szögfüggvények a térben, Gyakorlat
Hivatkozás(ok):Feladatok: 1971/szeptember: 1377. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tükrözzük a gúlát az ABCD négyzet síkjára. Mint tudjuk, a tükrözés távolságtartó és szögtartó leképezés, mely a négyzetlap pontjaihoz önmagukat rendeli. Az M pont M' képét az A, B, C, D pontokkal összekötve az eredeti gúla tükörképét kapjuk. Mivel a gúla szabályos, az oldalélei egyenlő hosszúak, az MM' egyenes átmegy az alap középpontján, így az MAM'C és MBM'D négyszögek rombuszok, tehát MC párhuzamos M'A-val és MB párhuzamos M'D-vel. Ezért a BMC sík párhuzamos a 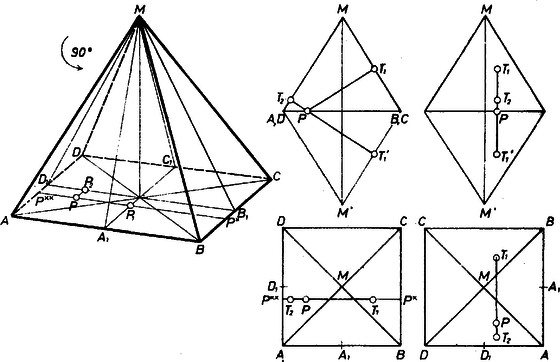DM'A síkkal.
A P-ből a BMC és AMD lapok síkjára állított merőlegesek talppontját jelöljük T1-gyel, ill. T2 vel, a T1-nek az ABCD síkra vonatkozó tükörképe pedig legyen T'1. (E pontok természetesen nem lesznek bármely P esetében az MBC, MAD, M'BC háromszög kerületén belül; az ábrán mind beleesnek). A tükrözés miatt PT1=PT'1, T1' rajta van a BM'C síkon és a PT'1 egyenes merőleges erre, tehát a vele párhuzamos MAD-re is, vagyis T1' a PT2 egyenesbe esik. Így a PT2+PT1=T2T'1 távolság egyenlő a DMA és BM'C síkok távolságával, ami független a P pontnak az ABCD négyzet belsejében vagy a kerületén elfoglalt helyzetétől.
Ugyanígy a P pontnak az AMB és CMD síkoktól mért távolságának összege egyenlő az AMB és CM'D párhuzamos síkok távolságával. Ugyanis a gúlát az MM' tengely körül 90∘-kal elforgatva a DMA sík átmegy az AMB-síkba, a BM'C sík a CM'D síkba, tehát a két összeg egyenlő. Ezzel a feladat állítását igazoltuk.

 

 

II. megoldás. Könnyen visszavezethetjük a feladat állítását arra az ismert, síkbeli tételre, hogy az egyenlő szárú háromszög alapján felvett P pontnak a száraktól vett távolságösszege független a P pont helyzetétől és megegyezik az egyenlő szárú háromszög szárához tartozó magasság hosszával (gimn. I. o. tankönyv 321. old. 3. feladat).
Legyen az AB, BC, CA, AD él felezőpontja rendre A1, B1, C1, D1, így A1C1 és B1D1 a négyzet oldalfelezői. Legyen P vetülete ezekre P1, ill. P2, ekkor PP1 párhuzamos AB-vel és CD-vel, ezért az MAB, MCD síkokkal is, tehát P1 ugyanakkora távolságban van e síkoktól, mint maga P. E két távolságot az MA1C1 síkban mérjük, összegük az idézett tétel szerint egyenlő az MA1C1 háromszög A1-ből húzott magasságával.
Hasonlóan P-nek az MAD és MBC síkoktól vett távolságainak összege annyi, mint P2-nek e síkoktól, más szóval az MD1, MB1 egyenesektől mért távolságainak összege, ez pedig az MB1D1 háromszög D1-ből húzott magasságával egyenlő. A gúla szabályos volta miatt MA1C1 és MB1D1 közös magasságú egyenlő szárú háromszögek, egybevágók, így a két összeg egyenlő.
 
Megjegyzések. 1. A feladat megoldása óta már minden megoldó megismerte a szögfüggvények fogalmát, ezt felhasználva gépiesebben bizonyíthatjuk az állítást. A gúla mindegyik oldallapja ugyanakkora α hegyesszöggel hajlik az alaphoz. Legyen P vetülete a BC élen P*, az AD-n P**, ekkor
PT1+PT2=PP*sinα+PP**sinα=(PP*+PP**)sinα==P*P**sinα=ABsinα.



2. Az állítás az alapsíknak a négyzet kerületén kívül levő P pontjaira is érvényes lesz akkor, ha az ilyen pontok és a gúla oldallapjai közti távolságnak előjelet tulajdonítunk: pozitívnak vesszük a távolságot, ha P az oldallapsíknak ugyanazon az oldalán van, mint maga a gúla, és negatívnak, ha P-t a sík másik oldalán választjuk meg.
3. Az állítás ‐ és legutóbbi kiterjesztése is ‐ érvényes minden szabályos, 2n oldalú gúla esetében, az MAiAi+1 és MAn+iAn+i+1 oldallapokat véve egy párnak, ahol A1,A2,...,A2n az alapsokszög egymás utáni csúcsai, i=1,2,...,n és A2n+1-et azonosnak tekintjük A1-gyel.