Kezdőlap


Feladat:	1371. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1972/március, 116 - 118. oldal		PDF \| MathML
Témakör(ök):	Középpontos tükrözés, Magasságpont, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1971/május: 1371. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az $A B C = H$ háromszög magasságpontját $M$ -mel, az $A B_{1} C_{1}$ , a $B C_{1} A_{1}$ és $C A_{1} B_{1}$ háromszög adott magasságpontját pedig rendre $A_{2}$ -vel, $B_{2}$ -vel, $C_{2}$ -vel.

1. Ha

H

-ban a

C

csúcsot

M

-re cseréljük, az új,

A B M

háromszög talpponti háromszöge ismét

A_{1} B_{1} C_{1}

lesz, hiszen

M

-nek és

C

-nek

A B

-n levő vetülete azonos, és

A B_{1} ⊥ B M

B A_{1} ⊥ A M

alapján az

A

és

B

csúcsoknak a szemközti oldalon levő vetülete

B_{1}

, illetve

A_{1}

lesz. (1. ábra).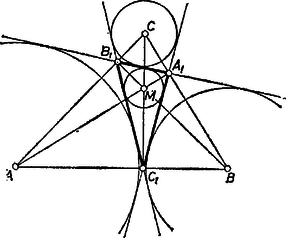

1. ábra

A mondottakból az is következik, hogy az

A B M

háromszög magasságpontja

C

. Kivétel csak az az eset, ha

H

-ban

A

-nál vagy

B

-nél derékszög van, hiszen ekkor az

A

B

M

pontok nem határoznak meg háromszöget. Ha viszont

H

nem derékszögű, akkor az

A

B

C

M

pontok különbözők, és bárhogy választunk ki e négy pont közül hármat, az ezek által alkotott háromszög magasságpontja a negyedik, és e háromszög talpponti háromszögének a helyzete nem függ attól, melyik három pontot választottuk az

A

B

C

M

közül. (A 3 talppont szerepe azonban cserélődik.) Ha

H

hegyesszögű, akkor az

A B M

B C M

C A M

háromszögekben

M

-nél tompaszög van ‐ pl.

A M B ∢ = 180^{\circ} - A C B ∢

‐, ha pedig

H

-ban valamelyik csúcsnál tompaszög van, akkor azt

M

-re cserélve hegyesszögű háromszöget kapunk.

H

hegyesszögű háromszög, akkor magasságvonalai az

A_{1} B_{1} C_{1} = H_{1}

talpponti háromszögben szögfelező egyenesek, hiszen a kerületi szögek és a merőleges szárú szögek tételei alapján például

A_{1}

-ben:

A A_{1} C_{1} ∢ = A C C_{1} ∢ = A B B_{1} ∢ =

= A A_{1} B_{1} ∢

; ennélfogva

H

oldalai pedig

H_{1}

-nek külső szögfelezői. Ha

H

-ban ‐ mondjuk

C

-nél ‐ tompaszög van, akkor az

A B M

háromszög hegyesszögű, tehát ennek a magasságvonalai lesznek

H_{1}

belső szögfelelezői, vagyis

H_{1}

-re nézve az

A C

B C

oldal belső, az

A B

pedig külső szögfelező. Ezek szerint ha

H

nem derékszögű, akkor az

A_{1}

B_{1}

C_{1}

M

pontok különbözők, nincs köztük három egy egyenesen levő pont, és

M

H_{1}

háromszög oldalegyeneseit érintő valamelyik kör középpontja,

H

csúcsai pedig a másik három érintőkör középpontjai.

2. Az

A B_{1} C_{1}

háromszög

A

-ban összefutó oldalai a

H

-ban is oldalak, ezért

A_{2}

magasságpontja a

B_{1}

-en át

C C_{1}

-gyel,

C_{1}

-en át

B B_{1}

-gyel párhuzamosan húzott egyenesek metszéspontja, tehát

B_{1} A_{2}

párhuzamos és egyenlő

M C_{1}

-gyel, ugyanígy

C_{1} A_{2} # M B_{1}

, másképpen mondva: az

{\vec{M A}}_{2}

vektor az

{\vec{M B}}_{1}

M C_{1}

vektorok összege (2. ábra):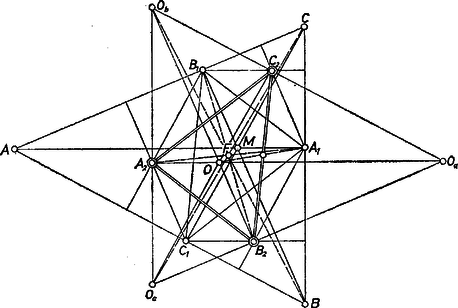

\begin{matrix} {\vec{M A}}_{2} = {\vec{M B}}_{1} + {\vec{M C}}_{1} . \end{matrix}

2. ábra

Hasonlóan

\begin{matrix} {\vec{M B}}_{2} = {\vec{M A}}_{1} + {\vec{M C}}_{1}, és {\vec{M C}}_{2} = {\vec{M A}}_{1} + {\vec{M B}}_{1} . \end{matrix}

Mérjük fel

M

-ból kiindulva az

({\vec{M A}}_{1} + {\vec{M B}}_{1} + {\vec{M C}}_{1})

vektort, legyen a végpontja

O

, az

M O

szakasz felezőpontja pedig

F

. Ekkor

\begin{matrix} \vec{M F} = \frac{1}{2} ({\vec{M A}}_{1} + {\vec{M B}}_{1} + {\vec{M C}}_{1}) = \frac{1}{2} ({\vec{M A}}_{1} + {\vec{M A}}_{2}), \end{matrix}

tehát

F

A_{1} A_{2}

szakasz felezőpontja, és hasonlóan mutatható meg, hogy

F

B_{1} B_{2}

C_{1} C_{2}

szakaszokat is felezi.

Ezek szerint az

A_{2} B_{2} C_{2} = H_{2}

háromszög az

F

pontra vonatkozó tükörképe a

H_{1}

-nek, és

O

M

tükörképe. Ezek alapján

O

H_{2}

oldalegyeneseit érintő 4 kör valamelyikének a középpontja,

H

csúcsainak az

F

-re vonatkozó tükörképe pedig

H_{2}

további három érintőkörének a középpontja. A centrális szimmetriából az is következik, hogy

F

H_{2}

háromszögből ugyanúgy állítható elő, mint

H_{1}

-ből:

\begin{matrix} \vec{O F} = \frac{1}{2} ({\vec{O A}}_{2} + {\vec{O B}}_{2} + {\vec{O C}}_{2}) . \end{matrix}

3. Ezek szerint ha az

A_{2}

B_{2}

C_{2}

pontok különbözők (és nincsenek egy egyenesen), akkor a szerkesztés menete a következő. Megrajzoljuk az

A_{2} B_{2} C_{2}

háromszög belső és külső szögfelezőit, a kapott négy metszéspont közül egyiket

O

-nak választjuk, a másik három közül az

O A_{2}

O B_{2}

O C_{2}

egyeneseken levőt pedig rendre

O_{a}

-val,

O_{b}

-vel,

O_{c}

-vel jelöljük. Majd tükrözzük

O

-t a

B_{2} C_{2}

szakasz felezőpontjára, kapjuk az

A_{1}

pontot; az

A_{1} A_{2}

szakaszt megfelezzük, kapjuk az

F

pontot. Végül az

O_{a} O_{b} O_{c}

háromszöget

F

-re tükrözve kapjuk a keresett

A B C

háromszöget.

4. Ezzel az eljárással négy különböző, a követelményeknek megfelelő háromszöget kapunk. (A 2. és 3. ábrán ezek közül egyet‐egyet rajzoltunk meg.)^{$^{*}$}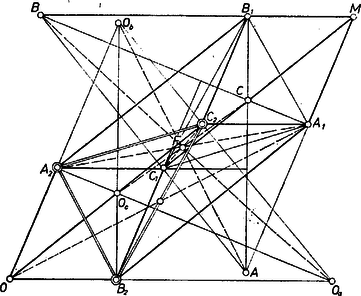

3. ábra

Valóban, a szerkesztés szerint az

O_{a} O_{b} O_{c}

háromszög talpponti háromszöge

A_{2} B_{2} C_{2}

, magasságpontja

O

, és

\begin{matrix} \vec{O F} = \frac{1}{2} ({\vec{O A}}_{2} + {\vec{O A}}_{1}) = \frac{1}{2} ({\vec{O A}}_{2} + {\vec{O B}}_{2} + {\vec{O C}}_{2}) . \end{matrix}

Legyen a

B_{2}

C_{2}

O

pontok

F

-re vonatkozó tükörképe

B_{1}

C_{1}

M

, akkor a tükrözés alapján az

A B C

háromszög magasságpontja

M

, és talpponti háromszöge

A_{1} B_{1} C_{1}

, továbbá

\begin{matrix} \vec{M F} = \frac{1}{2} ({\vec{M A}}_{1} + {\vec{M B}}_{1} + {\vec{M C}}_{1}) . \end{matrix}

Ebből pedig a 2. pontban mondottak szerint következik, hogy az

A B_{1} C_{1}

B C_{1} A_{1}

C A_{1} B_{1}

háromszögek magasságpontja rendre az adott

A_{2}

B_{2}

C_{2}

pont.

5. Ha tehát az eredeti

H

háromszög nem derékszögű, az adott három magasságpont mindig valódi

H_{2}

háromszöget határoz meg, és egy valódi (nem elfajult)

H_{2}

háromszögből négy különböző

H

háromszöget állíthatunk vissza. (Az "eredeti''

H

háromszöget csak akkor tudnánk egyértelműen rekonstruálni, ha azt is tudnánk róla, hogy van-e tompaszöge, és ha van, melyik csúcsánál van az. Ehhez hozzáértjük, hogy az adott három pont meg van betűzve, azaz szerepük előre meg van határozva.)

6. Ha

H

-ban ‐ mondjuk a

C

csúcsnál ‐ derékszög van, akkor az

A_{1}

B_{1}

M

pontok azonosak

C

-vel, tehát az

A_{1} B_{1} C

háromszög három csúcsa azonos. Így a

C_{2}

magasságpont nem értelmezhető,

H_{2}

nem jön létre. Az adott magasságpontokból eszerint csak akkor szerkeszthetünk megfelelő háromszöget, ha azok valódi háromszöget határoznak meg. (Akkor sem mondhatunk mást, ha

C \equiv A_{1} \equiv B_{1}

esetén

C_{2}

-t

C

-vel azonosnak definiáljuk. Ekkor ugyan megengedhető, hogy

H_{2}

két csúcsa ‐ mondjuk

A_{2}

és

B_{2}

‐ azonos legyen, de ekkor végtelen sok megfelelő

H

háromszög van, ezek egyik csúcsa a

C_{2}

-vel azonos

C

, a másik kettőt pedig egy tetszőleges, a

C_{2}

-n átmenő merőleges egyenespár metszheti ki az

A_{2} C_{2}

-re

A_{2}

-ben emelt merőleges egyenesből.)

^{$^{*}$}A két ábrán az

A_{2}

B_{2}

C_{2}

ponthármas egybevágó, csak az ábrák takarékos beállítása érdekében máshoz képest el vannak fordítva.