Kezdőlap


Feladat:	1369. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Párkány Katalin
Füzet:	1972/április, 158 - 162. oldal		PDF \| MathML
Témakör(ök):	Beírt tetraéder, Derékszögű háromszögek geometriája, Egyenes körkúpok, Koszinusztétel alkalmazása, Szabályos tetraéder, Gyakorlat
Hivatkozás(ok):	Feladatok: 1971/május: 1369. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a kúp csúcsát $M$ -mel, alapkörének a középpontját $O$ -val, a keresett tetraéder további csúcsait $A$ -val, $B$ -vel, $C$ -vel, az $A B C$ lap középpontját $K$ -val és a tetraéder élének hosszát $a$ -val. Mivel az $A$ , $B$ , $C$ csúcsok $O$ -tól $a$ távolságra vannak, ezek a csúcsok rajta vannak az $O$ középpontú, $a$ sugarú gömbön. Ha az $O M$ tengelyen átmenő tetszőleges síkkal metsszük a kúpot és a gömböt, a metszet egy szabályos háromszög, illetve egy $a$ sugarú kör lesz. Ez a kör a háromszög $M$ -en átmenő oldalát két pontban metszi, ha $a \leq \frac{1}{2}$ (és természetesen $a \geq \frac{\sqrt[]{3}}{4}$ ), egy pontban metszi, ha $\frac{1}{2} < a \leq \frac{\sqrt[]{3}}{2}$ , és nem metszi, ha $a > \frac{\sqrt[]{3}}{2}$ . Tehát ha $\frac{\sqrt[]{3}}{4} < a < \frac{\sqrt[]{3}}{2}$ , akkor a gömb a kúp palástját egy vagy két körben metszi. Nem lehet másrészt $a > \frac{1}{2}$ , mert akkor a metszetkör átmérője kisebb volna $a$ -nál, tehát nem tudnánk rajta elhelyezni három, egymástól páronként $a$ távolságra levő pontot.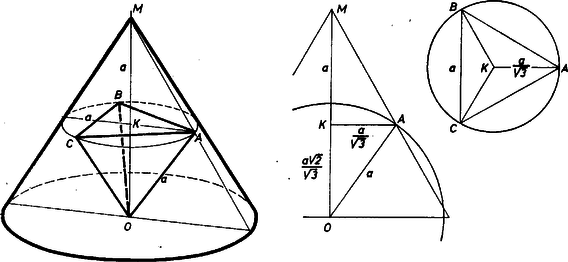

1. ábra

Ezek szerint

\frac{\sqrt[]{3}}{4} \leq a \leq \frac{1}{2}

, és az

a

sugarú gömb két körvonalban metszi a kúp palástját, amelyek síkja párhuzamos az alapsíkkal. Mivel a feladat nem kéri az összes megoldás megkeresését, célszerű a legegyszerűbb elrendezésben meghatározni

a

-t, amikor az

A

B

C

csúcsok ugyanazon a körvonalon vannak. Ekkor ez a kör az

a

oldalú szabályos

A B C

háromszög köré írható kör, tehát a sugara

a / \sqrt[]{3}

(1. ábra).
A

K

középpont rajta van az

O M

tengelyen, az

A K O

derékszögű háromszögben

\begin{matrix} K O^{2} = A O^{2} - A K^{2} = a^{2} - \frac{a^{2}}{3} = \frac{2}{3} a^{2} . \end{matrix}

Másrészt, mivel

A K

párhuzamos az alappal, a

K M : A K

arány értéke

\sqrt[]{3}

, tehát

M K = \sqrt[]{3}

A K = a

. Így a

\frac{\sqrt[]{3}}{2}

hosszú

M O

szakasz

M K

K O

darabjait kifejeztük

a

-val, amiből a meghatározható:

\begin{matrix} a \frac{\sqrt[]{2}}{\sqrt[]{3}} + a = \frac{\sqrt[]{3}}{2}, \\ a = \frac{3 (\sqrt[]{3} - \sqrt[]{2})}{2} = 0, 4768. \end{matrix}

Megjegyzések. 1. Megvizsgáljuk azokat az elrendezéseket is, amelyekben az

A

B

C

csúcsok közül kettő az egyik metszet‐körvonalon, egy a másikon van.

I. Tegyük fel először, hogy a két csúcsot tartalmazó körvonal sugara nagyobb, és legyenek ezen a körvonalon a

B

és

C

csúcsok. A

B C

él felezőpontját jelöljük

F

-fel, a

B

-n és

C

-n átmenő körnek az

M A

alkotón levő pontját

D

-vel (

F

A M O

síkban van, 2. ábra).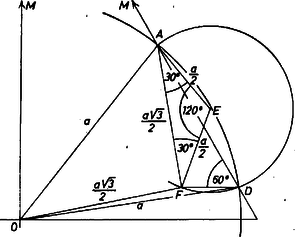

2. ábra

A F O

háromszög egyenlő szárú, alapja

a

, szárai

a \sqrt[]{3} / 2

hosszúak (lapbeli magasság). Mivel

D F

párhuzamos a kúp alapjával,

D

-ből az

A F

szakasz

60^{\circ}

-os szög alatt látszik, tehát

D

rajta van az

A F

feletti

60^{\circ}

-os látókörön, és az

A F

egyenes

O

-t nem tartalmazó oldalán van. Ennek a körnek az

E

középpontja az

A

F

pontoktól

a / 2

távolságra van, amiből az

E O

távolság meghatározható. A cosinustétel alapján az

A E O

háromszögben

\begin{matrix} E O^{2} = a^{2} + \frac{a^{2}}{4} - a^{2} cos E A O ∢ = a^{2} {\frac{5}{4} - cos (F A O ∢ + 30^{\circ})} = \end{matrix}

\begin{matrix} = a^{2} {\frac{5}{4} - cos F A O ∢ \cdot cos 30^{\circ} + sin F A O ∢ \cdot sin 30^{\circ}} = a^{2} {\frac{5}{4} - \frac{1}{\sqrt[]{3}} \cdot \frac{\sqrt[]{3}}{2} + \frac{\sqrt[]{2}}{\sqrt[]{3}} \cdot \frac{1}{2}} = \frac{9 + 2 \sqrt[]{6}}{12} a^{2} . \end{matrix}

Az egyenlő szárú

A D O

háromszög szárai

a

hosszúságúak, az

A D

alaphoz tartozó

m

magasság hossza

\begin{matrix} m = a cos A O E ∢ = a \frac{A O^{2} + E O^{2} - A E^{2}}{2 A O \cdot E O} = a \frac{\frac{3}{4} + λ^{2}}{2 λ}, \end{matrix}

ahol

\begin{matrix} λ = \sqrt[]{\frac{9 + 2 \sqrt[]{6}}{12}} . \end{matrix}

Az egységnyi oldalú szabályos háromszögben az alap

O

felezőpontjának a másik két oldaltól való távolsága

m = \frac{\sqrt[]{3}}{4}

, tehát

\begin{matrix} a = \frac{2 \sqrt[]{3} λ}{3 + 4 λ^{2}} = \sqrt[]{\frac{9 + 2 \sqrt[]{6}}{{[3 + \frac{1}{3} (9 + 2 \sqrt[]{6})]}^{2}}} = \sqrt[]{\frac{81 + 18 \sqrt[]{6}}{{(18 + 2 \sqrt[]{6})}^{2}}} = \\ = \frac{\sqrt[]{567 + 12 \sqrt[]{6}}}{50} = 0, 4884. \end{matrix}

II. Ha pedig

A

van a nagyobbik körön és

B

C

a kisebbiken, akkor az

A D F

szög

120^{\circ}

-os,

E

A D

egyenes

O

-t tartalmazó oldalán van (3. ábra) és a fentihez hasonló számolással kapjuk, hogy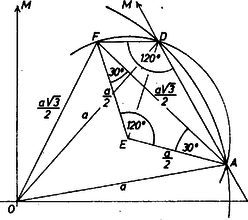

\begin{matrix} E O^{2} = \frac{9 - 2 \sqrt[]{6}}{12} a^{2} \\ a = \frac{\sqrt[]{567 - 12 \sqrt[]{6}}}{50} = 0, 4637. \end{matrix}

3. ábra

A három elrendezésnél

a

-ra kapott értékek igen közel vannak egymáshoz. Jobb áttekintés érdekében a 2. és 3. ábra nem mérethű.
A ferdén behelyezett tetraéderek élére közelítő értéket adott Párkány Katalin (Budapest, Berzsenyi D. Gimn., II. o.t.),

+ 2

pontot kapott.

2. A beírt tetraéderek

A

B

C

csúcsai a kúp kiterített palástján könnyen megszerkeszthetők, felhasználva a fent kapott méreteket és hogy a kúp alkotója éppen 2-szer akkora, mint az alapkör sugara. Így ugyanis a palást kiterítése félkörlemez, a kúpnak az alappal párhuzamos síkban levő körei a kiterítésben kétszer akkora sugarú félkörök, és minden ilyen kör bármely ívéhez a kiterítésben feleakkora középponti szög tartozik, mint az eredetiben.
A ferde tengellyel beírt tetraéder I. esetében az

O M A

, ill.

O M B

háromszögből a cosinustétellel

M A_{1} = (18 - 2 \sqrt[]{6}) / 25

M B_{1} = M C_{1} = (39 + 4 \sqrt[]{6}) / 50

, és a

B

C

pontokat tartalmazó körmetszet sugara

r_{1} = (39 + 4 \sqrt[]{6}) / 100

, e körben az

a

hosszúságú

B_{1} C_{1}

húrnak a

K_{1}

középponttól való távolsága

d_{1} = (6 + \sqrt[]{6}) / 20

, és a

B_{1} K_{1} C_{1} = 2 φ

szögre

cos φ = d_{1} / r_{1} = (14 + \sqrt[]{6}) / 19

, tehát

M A_{1}

M B_{1}

cos φ

megszerkeszthetők

(φ = 30^{\circ} 2')

és a kiterítésben

B_{1} M C_{1} ∢ = φ

és

A_{1}

rajta van

B_{1} C_{1}

felező merőlegesén (4. ábra).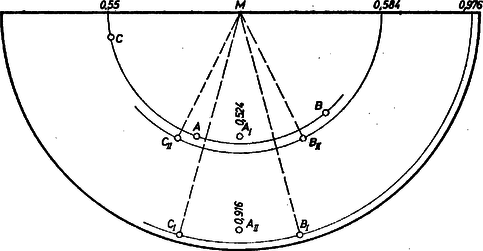

4. ábra

Hasonlóan adódik a II. esetben

B_{II}

C_{II}

A_{II}

kölcsönös helyzete.