Feladat: 1363. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Kósa Zsuzsanna 
Füzet: 1971/október, 67 - 68. oldal  PDF  |  MathML 
Témakör(ök): Derékszögű háromszögek geometriája, Háromszögek nevezetes tételei, Logikai feladatok, Szögfüggvények, síkgeometriai számítások, Gyakorlat
Hivatkozás(ok):Feladatok: 1971/április: 1363. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az állítások igaz, ill. hamis voltára vonatkozó közlést csak úgy tudjuk felhasználni, ha egyenként sorra vesszük az igaz állítások párjaira lehetséges eseteket.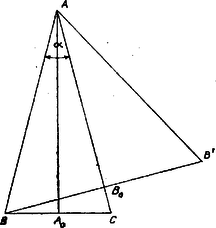
1. Próbáljuk fölvenni, hogy III. és IV. igazak. Ekkor AB=AC=2BC=2, a háromszög egyenlő szárú, így sem az alapján, nincs derékszög, sem a szárai közt, hiszen BC<AB alapján α=BAC∢<ACB∢<90∘; eszerint I. hamis (1. ábra).

 
 
1. ábra
 

Továbbá a háromszög tengelymagassága AA0=15/2, a szárakra merőleges magasságok fele ekkorák, hiszen két magasság aránya bármely háromszögben a megfelelő oldalak arányának reciprokával egyenlő, így sinα=15/8≠1/2=sin30∘, tehát α≠30∘, II. is hamis. (Másképpen így mondhatjuk ezt: BB0=15/4, így BB'=15/2<2=AB=AB' ‐ ahol B' a B-nek AC-re való tükörképe, ezért BAB'∢<ABB'∢=AB'B∢, így BAB'∢<60∘,BAC∢<30∘.) Így a hamis állítások száma 2, amint a feladat állítja, találtunk egy megfelelő ABC háromszöget, és ennek kerülete 5 egység.
2. Ha a III.-at és a II.-at próbáljuk igaznak venni, akkor a háromszöget megszerkeszthetjük. Egy A csúcsú 30∘-os szög egyik szárára AB=2 egységet mérünk fel, majd B körül BC=1 sugárral kört írunk, ekkor C csak az ív és a másik szár közös pontja lehet (2. ábra).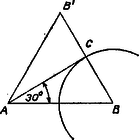
 
 
2. ábra
 

Megmutatjuk, hogy csak egy közös pontjuk van, vagyis érintkeznek, így pedig a BCA szög derékszög, I. igaz, a közléssel ellentétben, tehát ez a háromszög nem felel meg. Valóban, a másik szár és a kör közös pontja rajta van a körnek a másik szárra vonatkozó tükörképén is, a B' körüli, 1 sugarú körön, ahol B'AB∢=2⋅30∘ és B'A=BA=2. Így pedig B'AB szabályos háromszög, BB'=2, a két kör éppen érinti egymást és az AC egyenest, amint állítottuk.
3. Ugyanígy nem felel meg az ABC háromszög, ha a IV.-et és a II.-t vesszük igaznak, hiszen ez az eset B és C cseréjével az előbbibe megy át, így B-nél volna derékszög.
4. III. állítás mellé az I.-t véve igaznak, az ABC háromszög megfelel, ha a derékszög csúcsának B-t vesszük (3. ábra).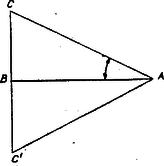
 
 
3. ábra
 

Így ugyanis AC=BC2+BA2=5≠2, tehát IV. hamis; másrészt
tgBAC∢=12<13=tg30∘,A∢<30∘,
vagyis II. is hamis, ugyanis a tangensfüggvény a 0∘, 90∘ intervallumban minden értéket, amit fölvesz, csak egy helyen vesz föl. (Mondhatjuk így is: BAC∢<30∘, mert C-nek BA-ra vonatkozó tükörképét C'-vel jelölve, az ACC' háromszögben AC=AC'>CC', emiatt CAC'∢<ACC'∢=AC'C∢, és így CAC'∢<60∘, CAB∢<30∘.) A talált háromszög kerülete 3+5 egység.
Ha viszont (tovább is III. és I. igaz volta esetében) C-t vesszük a derékszög csúcsának, a föntiekhez hasonlóan látható, hogy BAC∢=30∘, II. is igaz, tehát a háromszög nem felel meg. ‐ Végül nem kell próbálnunk A-ba tenni derékszöget, hiszen BC<AB alapján BAC∢<ACB∢, és így BAC∢<90∘.
5. Lényegében a legutóbbi esetre jutunk, ha a IV.-et és az I.-t vesszük igaznak, csupán B-t és C-t kell fölcserélnünk: ha ACB∢=90∘ és AC=2BC, akkor A∢<30∘ és AB=5, II. és III. hamis, a kerület 3+5.
6. Végül olyan ABC háromszög sem felelhet meg, melyben II. és I. igaz: BAC∢=30∘ és vagy B-nél vagy C-nél derékszög van, mert ekkor igaz IV., ill. III. is. Más lehetőség nincs a két igaz állítás megválasztására.
Mindezek szerint az I.‐IV. állítások és a ,,2 igaz, 2 hamis'' közlés alapján megfelelő háromszög kerülete lehet 5 és lehet 3+5 egységnyi.
 

Kósa Zsuzsanna (Budapest, Móricz Zs. Gimn., I. o. t.)