Feladat: 1359. matematika gyakorlat Korcsoport: 14-15 Nehézségi fok: nehéz
Megoldó(k):  Bara T. ,  Bartolits I. ,  Bezdek K. ,  Császár Gy. ,  Fórizs Erzsébet ,  Frey G. ,  Hasenfratz Anna ,  Horváth Mária ,  Kiss E. ,  Kollár J. ,  Lakner P. ,  Lóska A. ,  Nagy Cs. ,  Németh Gy. ,  Oláh Vera ,  Oszvald K. ,  Párkány Katalin ,  Pócsi Gy. ,  Prőhle P. ,  Szalay I. 
Füzet: 1971/október, 62 - 64. oldal  PDF  |  MathML 
Témakör(ök): Hatszög-rácsok geometriája, Gyakorlat
Hivatkozás(ok):Feladatok: 1971/március: 1359. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Először leírjuk a hálózat felhasználandó tulajdonságait. A szabályos hatszög szögei 120∘-osak, ezért minden csomópontból 360∘:120∘=3 db egységszakasz ‐ él ‐ indul ki, éspedig a hálózatra alkalmasan rátett óraszámlap 0 órás, 4 és 8 órás osztópontjába mutató sugarakkal párhuzamosan, vagy az ezekkel ellentétes irányú (6, 10 és 2 órás) sugarakkal párhuzamosan. Az előbbieket C0, az utóbbiakat C6 típusú csomóknak nevezhetjük. Minden csomópont 3 szomszédja vele ellentétes típusú. Bármely két ellentétes típusú csomó élhármasa egymásnak tükörképe a két csomó közti szakasz felezőpontjára nézve (1. ábra), ennélfogva a velük szomszédos 3‐3 csomópont is egymásba megy át, a mondott tükrözéssel, és továbbmenve ugyanez az egész hálózatra is áll.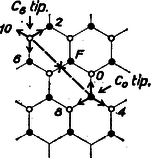

 
 
1. ábra
 

Megmutatjuk, hogy ha a hálózatnak egy az A-ból B-be vezető útvonala tartalmaz olyan két párhuzamos egységszakaszt, melyeken a haladási irány ellentétes, akkor ennél az útvonalnál rövidebb útvonal is vezet a hálózat mentén A-ból B-be (2. áb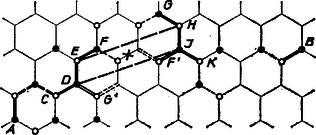ra).
 
 
2. ábra
 

Legyen az U=A...CDEF...GHJK...B útvonalban szereplő DE és HJ él párhuzamos, bejárásuk pedig ellentétes irányú. Ekkor D és J egyező típusú csomók, E és H velük ellentétes típusúak. S mivel még DE=JH, azért a DEHJ négyszög paralelogramma, ennek középpontjára tükrözve U-nak EF...GH részét, a JF'...G'D kép minden egyes egységszakasza éle a hálózatnak. Eszerint az A...CDG'...F'JK...B útvonal a hálózat mentén halad, másrészt 2 egységgel rövidebb, mint U. Állításunkat bebizonyítottuk.
Eszerint a feladat föltevése ‐ hogy ti. A és B közt nincs 20 egységnél rövidebb út ‐ egyértelmű azzal, hogy a bogár által használt útvonalat a csomókkal egységvektorokra osztva, benne legföljebb 3 különböző irányú vektort találunk. És mivel A-tól B-ig váltakozva ellentétes típusú csomópontokon haladtunk át, azért a lehetségesnek talált 3 irány közül egyik a C0, egy másik a C6 típusú csomók irányai közül való. A harmadik irány ‐ ha egyáltalán van 3 irány ‐ ismét valamelyik csomótípus irányai közé tartozik, ezért egy legrövidebb útvonalban a másik típusú csomók 3 iránya közül csak egy szerepel, ezekből a csomókból mindig ugyanabban az irányban kellett tovább haladnunk. Így az A-ból B-be vivő 20 (vagyis páros számú) egységnyi úton vagy a páratlan sorszámú, vagy a páros sorszámú élek bejárási iránya mindenesetre egyezik. Ezzel az állítást bebizonyítottuk.
A sorszámokra kimondott megállapítás többlet az állításhoz képest, de nyilvánvaló, hiszen két egymás utáni egységnyi lépés iránya nem lehet egyező. Azt is látjuk, hogy az állítás akkor is érvényes, ha 20 helyett bármely (pozitív) páros számot mondunk. (Ha viszont az útvonal hossza páratlan szám, akkor az állításnak nyilvánvalóan nincs értelme.)
 

Megjegyzések. 1. A 3. ábra a C csomópontból 2, 4 és 6 egységnyi útvonallal elérhető csomópontokat mutatja.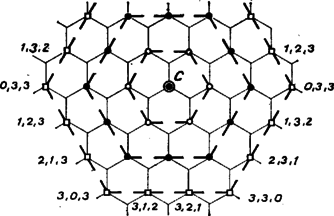
 
 
3. ábra
 

Mindegyik ilyen csomót a hozzá legközelebbi ugyanilyen csomóval összekötve olyan szabályos hatszögeket kapunk ‐ C-vel mint középponttal ‐, amelyeknek oldala rendre 1-szer, 2-szer, 3-szor akkora, mint az eredeti hatszöges hálószem rövidebb átlója. E hatszögek bármelyik oldalának egy csomójába úgy jutunk C-ből, hogy rendre 1, 2, ill. 3 lépésben az illető oldalra merőlegesen haladunk; így a hatszög csúcsaiba vivő (legrövidebb) útvonalakon csak két irányban mozgunk, váltakozva. A beírt számhármasok azt adják, hogy az addigi 6 lépés közül rendre hány volt párhuzamos az óraszámlap 0‐6, ill. 4‐10, ill. 8‐2 átmérőjével.
2. Könnyű leolvasni azt is a 3. ábráról, hogy a hálózat két pontja között általában több olyan útvonal lehetséges, amelynél nincs rövidebb. A most mondott hatszögek csúcsaiba azonban csak 1 ilyen vezet. ‐ Azt is mutatja a szemlélet, hogy bármelyik legrövidebb útvonalnak minden éle mentén a szokásos értelemben is közelebb jut a bogár a végponthoz, minden élnek van komponense ebben az irányban.
II. megoldás. A hálózat egyes szakaszainak három különböző állásuk van, az azonos állásúak egymással párhuzamosak. Fessük ki a hálózat szakaszait három különböző színnel, pirossal, kékkel és fehérrel úgy, hogy az azonos állásúak színe azonos legyen. (A 4. ábrán a piros színt pontozott, a kéket kettős, a fehéret folytonos vonal jelöli, alább a típusokat kezdőbetűjükkel ‐ p-vel, k-val, f-fel ‐ jelöljük.)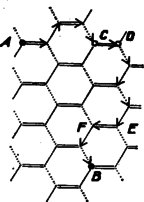
 
 
4. ábra
 

Ha le akarjuk írni a hálózat valamely útvonalát, elegendő annak kezdőpontját megadni, és ettől kezdve az egyes útszakaszok típusát felsorolni abban a sorrendben, ahogy végigmegyünk rajtuk. (Például a 4. ábra nyilakkal jelzett AB útvonalának a leírása: (A) kfk pkp fpf kfp.) Ha megadjuk a p, k, f betűk egy tetszőleges sorozatát, az tetszőleges kezdőpont-választás mellett megadja a hálózat egy lehetséges útvonalát, hiszen a hálózat minden útelágazásánál mindhárom állású szakasz egyszer és csakis egyszer fordul elő.
Vizsgáljuk meg, hogyan állapíthatjuk meg egy útvonal ilyen leírása alapján, hogy az legrövidebb-e a végpontjait összekötő (hálózati) útvonalak közül.
a) Egy minimális útvonal leírásában nem fordulhat elő ugyanaz a betű kétszer egymás után, hiszen ez azt jelentené, hogy ugyanazon az útszakaszon oda-vissza megyünk végig. (Az ilyen betűismétlést tartalmazó útleírás rövidíthető azzal, hogy a kettősen előforduló betűt elhagyjuk.) Tehát egy minimális útvonal leírásában a szomszédos betűk mindig különbözőek.
b) Általánosítjuk az a) alatti szabályt. Sorszámozzuk meg az útleírásban előforduló betűket az út kezdetétől 1-gyel, 2-vel, 3-mal s í.t. (Például az előbb említett útvonal ötödik szakasza k.) Azt állítjuk, hogy egy minimális útvonal leírásában az azonos betűkhöz rendelt sorszámok paritása megegyezik (azaz vagy csupa páros, vagy csupa páratlan sorszámuk van az azonos betűknek). Tegyük fel állításunkkal ellentétben, hogy egy minimális út leírásában van olyan betű, amely páratlan és páros sorszámmal is előfordul. Legyen mondjuk ez a k betű, akkor van az útleírásnak egy olyan része, amely mondjuk egy páratlan sorszámú k-val kezdődik, egy páros sorszámú k-val végződik, és e két k között más k nem fordul elő. (A példabeli útvonal számozása a következő:
kfkpkpfpfkfp123456789101112
ennek az 5, és a 10. betűje közti része ilyen.) Az a)-szabály szerint e két k betű között a p és f betűk felváltva követik egymást, mondjuk a p betűk sorszáma páros, és az f-eké páratlan. Jelöljük az első k betűnek megfelelő útszakasz kezdőpontját C-vel, végpontját D-vel, a második k szakasz kezdőpontját E-vel, végpontját F-fel. A C, D, E, F pontok egy téglalap csúcsai a felsorolásuk sorrendjében, hiszen a szomszédos (p,f) útszakasz-párok kezdő és végpontját összekötő egyenes merőleges a k-val jelzett útszakaszokra, és a D és E közötti útvonal ilyen (p,f) párokból áll. E téglalap C és F csúcsa viszont összeköthető a CD...EF útvonalnál két egységgel rövidebb (C),f,p,...,f,p útvonallal is, amely annyi (f,p)-párból áll, ahány (p,f) pár kötötte össze a D és E pontokat. A vizsgált útvonal tehát nem minimális, eredeti állításunkat ezzel bebizonyítottuk.
Ezek alapján a feladat állításánál általánosabban azt bizonyítjuk, hogy ha a háló valamely A és B csomópontja közti minimális útvonal páros sok útszakaszból áll, akkor az útszakaszok fele azonos típusú. Valóban, ezeknek az útszakaszoknak a fele páratlan, fele páros sorszámú. A b)-szabály szerint a k-val jelzett útszakaszok mindegyike vagy páros vagy páratlan sorszámú. Legyenek ezek ‐ mondjuk ‐ páratlan sorszámúak. (A menetirány megfordításával mindenesetre elérhető ez.) Ha mármost a p-vel és f-fel jelzett útszakaszok mindegyike páros sorszámú, akkor az útszakaszok fele k-val jelzett. Ha pedig van köztük páratlan sorszámú, akkor minden páros sorszámú útszakasz a másik színnel jelzett, az állítás ebben az esetben is igaz.