Kezdőlap


Feladat:	1358. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1971/szeptember, 21 - 24. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Középpontos tükrözés, Merőleges affinitás, Párhuzamos szelők tétele, Síkgeometriai számítások trigonometria nélkül sokszögekben, Egyéb sokszögek geometriája, Aranymetszés, Térelemek és részeik, Gyakorlat
Hivatkozás(ok):	Feladatok: 1971/március: 1358. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. a) Az oldalak és átlók párhuzamos párokba állítása egyértelmű, mert az $A B C D E$ ötszögben pl. az $A B$ oldallal csak a $C E$ átló lehet párhuzamos, hiszen a többi $4$ átló kettesével $A$ -ból és $B$ -ből indul ki ( $1$ . ábr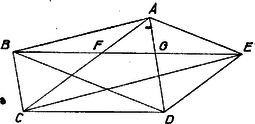a).

1. ábra

Elég lesz bizonyítani, hogy

A D : B C = A C : E D

, vagyis hogy két ugyanazon csúcsból kiinduló átló és a velük párhuzamos oldalak közti arány egyenlő. Ugyanis ötszögünknek egyik oldala sincs valamely tulajdonsággal megkülönböztetve a többiektől, így az adandó bizonyításban a betűk ciklikusan fölcserélhetők.

A

B

C

D

E

helyére rendre

C

D

E

A

B

-t írva eredményünkből

C A : D E = C E : B A

adódik, amit az előbbivel egybevetve

A D : B C = C E : B A

, vagyis a kérdéses arányok akkor is egyenlők, ha közös csúccsal nem bíró két átlót osztunk a velük párhuzamos oldallal. Eszerint az arány értéke mind az öt párhuzamos szakaszpárra nézve ugyanaz lesz.
Mármost a

B E

átlónak

A C

-vel és

A D

-vel való metszéspontját

F

-fel, ill.

G

-vel jelölve, a keletkezett paralelogrammákban

B C = G D

, ill.

F C = E D

, ennélfogva a párhuzamos szelők tételét az

C A D

szög száraira alkalmazva

\begin{matrix} \frac{A D}{B C} = \frac{A D}{G D} = \frac{A C}{F C} = \frac{A C}{E D}, \end{matrix}

amit bizonyítani akartunk.
b) Az öt arány közös

x

értékére a

B F

és

E F C

háromszögek hasonlósága alapján teljesül

\begin{matrix} x = \frac{B E}{C D} = \frac{B F + F E}{F E} = \frac{B F}{F E} + 1 = \frac{B A}{C E} + 1 = \frac{1}{x} + 1, \\ x^{2} - x - 1 = 0, x = \frac{\sqrt[]{5} + 1}{2} (= 1, 618), & (1) \end{matrix}

hiszen a konvexség folytán

F

belső pontja az ötszögnek, ezért

x = \frac{B E}{C D} > 1

, másrészt

(1)

másik gyöke negatív. Ezzel a megoldást befejeztük.

II. megoldás. Hosszabbítsuk meg mindegyik oldalt a vele nem szomszédos két oldalegyenessel való metszésig, és legyen a metszéspontok jele

A'

B'

C'

D'

E'

úgy, hogy ‐ a föltevés alapján ‐ az

A C A' D

B D B' E

C E C' A

D A D' B

és

E B E' C

négyszögek paralelogrammák. Így mindegyik oldalegyenes két új pontja egymás tükrös párja az illető oldal felezőpontjára nézve, pl.

C'

és

E'

A B

oldal felezőpontjára, hiszen

C' A # E C 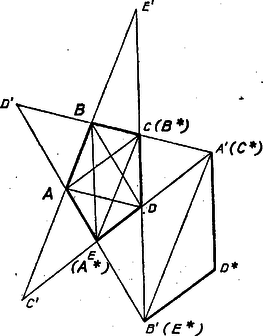# B E'

(

2

. ábra).

2. ábra

Ezek alapján az

A B

oldal és a vele párhuzamos átló

C E : A B = x

arányát egymás utáni párhuzamos vetítésekkel és tükrözésekkel átvihetjük az

A B

egyenes más két szakaszának arányába:

\begin{matrix} x = \frac{E C}{A B} = \frac{C D'}{B D'} = \frac{B A'}{C A'} = \frac{E A'}{D A'} = \frac{D C'}{E C'} = \\ = \frac{B C'}{A C'} = \frac{B A + A C'}{A C'} = \frac{B A + C E}{C E} = \frac{1}{x} + 1, \end{matrix}

eszerint

C E^{2} = A B (A B + C E)

x

-re pedig ismét a fenti

(1)

adódik.
Eredményünket az ötszögnek kizárólag a föltevés szerinti tulajdonságából kaptuk ‐ sőt a párhuzamosságok közül csak

4

-et használtunk fel (a

C D

és

B E

közöttit nem, hiszen nem szerepelt

B'

, sem

E'

) ‐ tehát az arány bármely ilyen ötszögben bármelyik átló és a vele párhuzamos oldal között ugyanekkora értékű.

III. megoldás. Tovább használjuk a II. megoldásban bevezetett jelöléseket. Nagyítsuk ki az

A B C D E

ötszöget a

D'

centrumból úgy, hogy az

A

csúcs képe

E

legyen, és jelöljük az új csúcsokat rendre

A^{*}

-gal,

B^{*}

-gal,

C^{*}

-gal,

D^{*}

-gal és

E^{*}

-gal. E jelölés szerint

A^{*}

azonos

E

-vel. Az

A B

egyenes képe az

A^{*}

-on átmenő,

A B

-vel párhuzamos egyenes, vagyis

E C

; másrészt

B^{*}

rajta van a

D' B

egyenesen, tehát

B^{*}

azonos

C

-vel. Az

A C

egyenes képe az

A^{*}

-on átmenő,

A C

-vel párhuzamos egyenes, vagyis

E D

; és mivel

C^{*}

rajta van a

D' C

egyenesen,

C^{*}

azonos

A'

-vel. Hasonlóan kapjuk, hogy

E^{*}

azonos

B'

-vel, abból pedig, hogy

D

E

-n, illetve

C

-n átmenő,

A C

-vel, illetve

B E

-vel párhuzamos egyenes metszéspontja, következik, hogy

D^{*}

B'

D

A'

pontokat paralelogrammává kiegészítő pont (

2

. ábra).
Az

A^{*} B^{*} C^{*} D^{*} E^{*}

ötszög

A^{*} B^{*}

oldala azonos az eredeti ötszög

E C

átlójával. Mivel

A D A' C

paralelogramma,

B^{*} C^{*}

egyenlő az

A D

átlóval, és hasonlóan kapjuk, hogy

A^{*} E^{*}

egyenlő

B D

-vel. Végül

C^{*} D^{*}

, illetve

D^{*} E^{*}

egyenlő

D B'

-vel, illetve

D A'

-vel, ezek pedig egyenlőek a

B E

, illetve

A C

átlókkal. Az

A B C D E

ötszög centrális hasonlóságából származó képének az oldalai tehát rendre egyenlőek az eredeti ötszög velük párhuzamos átlóival. Emiatt az eredeti ötszög bármely oldalának és a vele párhuzamos átlójának az aránya egyenlő az

A B C D E

A^{*} B^{*} C^{*} D^{*} E^{*}

ötszögek megfelelő oldalainak az arányával, ami minden oldalra ugyanaz az érték, hiszen nem más, mint az alkalmazott nagyítás aránya.
Rátérünk ennek az aránynak a meghatározására. Az előbb mondottakból következik, hogy például

\begin{matrix} C D : B E = C^{*} D^{*} : B^{*} E^{*}, \end{matrix}

ahol

C^{*} D^{*}

egyenlő

B E

-vel,

B^{*} E^{*}

pedig azonos

C B'

-vel, tehát egyenlő

C D

-nek és a

D B'

-vel egyenlő

B E

-nek összegével:

\begin{matrix} C D : B E = B E : (C D + B E) . \end{matrix}

Ebből az

x = \frac{B E}{C D}

hányadosra az (1)-gyel azonos

\begin{matrix} x = \frac{1}{x} + 1 \end{matrix}

másodfokú egyenletet kapjuk, melynek pozitív gyöke

x = \frac{1 + \sqrt[]{5}}{2}

IV. megoldás. Legyen

S_{2}

A B C D E

ötszög síkját az

A B

egyenesben metsző tetszőleges sík,

A' B' C' D' E'

pedig

S_{2}

-ben egy olyan szabályos ötszög, melynek

A'

, illetve

B'

csúcsa azonos

A

-val, illetve

B

-vel. Húzzunk párhuzamost

C

-n és

E

-n át a

D D'

egyenessel, és jelöljük ezek

S_{2}

-vel alkotott metszéspontjait

C^{*}

-gal, illetve

E^{*}

-gal. Azt fogjuk megmutatni, hogy

C^{*}

azonos

C'

-vel,

E^{*}

pedig

E'

-vel (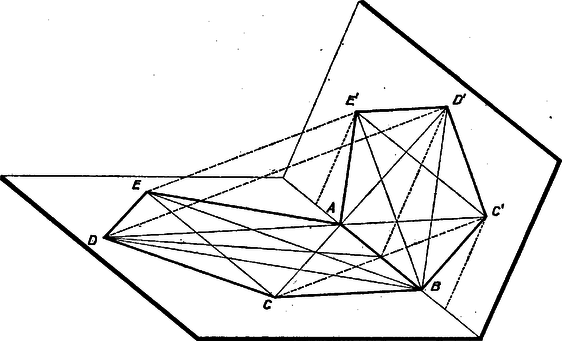

3

. ábra).

3. ábra

Mivel

E C ∥ A B

, az

E E^{*}

C C^{*}

egyenesek által meghatározott sík párhuzamos

A B

-vel, és ugyancsak párhuzamos

A B

-vel ennek a síknak az

S_{2}

-vel alkotott

E^{*} C^{*}

metszésvonala is.
Hasonlóan kapjuk

A E

és

B D

, illetve

B C

és

A D

párhuzamosságából, hogy

A E^{*} ∥ B D'

, illetve

B C^{*} ∥ A D'

, tehát

E^{*}

A E'

C^{*}

pedig a

B C'

egyenesen van. Mivel az

A B D'

háromszög egyenlő szárú, az

A B

egyenes

t

felező merőlegesére tükrözve a háromszög önmagába megy át, ez a tükrözés az

A B

-vel párhuzamos

C^{*} E^{*}

egyenest is önmagába viszi át, a

B C^{*}

egyenes képe pedig az

A E^{*}

egyenes. Ezek szerint

C^{*}

képe

E^{*}

, és

t

A B C^{*} D' E^{*}

ötszög szimmetriatengelye. A fentiekhez hasonlóan

C D

és

B E

párhuzamossága maga után vonja

C^{*} D'

és

B E^{*}

párhuzamosságát, ebből pedig következik (anélkül, hogy a

D E

és

A C

párhuzamosságára vonatkozó feltételt használnánk), hogy

D' E^{*}

és

A C^{*}

is párhuzamosak.
Ha a

C^{*}

E^{*}

pontokat úgy mozgatjuk a

B C'

A E'

félegyeneseken, hogy közben

C^{*} E^{*}

párhuzamos

A B

-vel, akkor

B

-től, illetve

A

-tól távolodva a

D' A C^{*}

szög monoton csökken, az

A D' E^{*}

szög monoton nő, tehát ez a két szög a

C^{*} E

egyenesnek csak egyetlen helyzeténél lehet egyenlő. Ez be is következik, ha

C^{*}

azonos

C'

-vel,

E^{*}

pedig

E'

-vel, tehát ekkor és csakis ekkor lehet

A C^{*}

párhuzamos

E^{*} D'

-vel, előrebocsátott állításunkat ezzel bebizonyítottuk.
Igaz a párhuzamos szelők tételének a következő általánosítása (melynek bizonyítását az olvasóra hagyjuk). Ha

P Q

és

R S

párhuzamos szakaszok az

S_{1}

síkban, és a végpontjaikon át

S_{2}

-t metsző, egymással párhuzamos egyeneseket fektetünk, melyek

S_{2}

-t rendre a

P'

Q'

R'

S'

pontokban metszik, akkor

P Q : R S = P' Q' : R' S'

. Emiatt az

A B C D E

ötszög oldalainak a velük párhuzamos átlóival alkotott aránya egyenlő az

A B C' D' E'

ötszög megfelelő szakaszainak az arányával, ami

(\sqrt[]{5} + 1) : 2

Megjegyzések. 1. A IV. megoldás módszerével könnyen bizonyítható, hogy ha

A

B

D

a sík tetszőleges pontjai (melyek nincsenek egy egyenesen), akkor mindig található egy és csakis egy

C

E

pontpár a síkon úgy, hogy az

A B C D E

ötszögre teljesüljenek a feladat feltételei. Azt is láttuk a II. és a IV. megoldásban, hogy elegendő 4 átló-oldal-pár párhuzamosságát feltenni, ebből már következik az ötödik pár arányának egyezése és párhuzamos volta.
2. A II. és a III. megoldásban azt kaptuk, hogy a vizsgált ötszögek oldal : átló aránya egyenlő az átló: (oldal+átló) arányával. Azt mondjuk, hogy ha egy kisebb és egy nagyobb szakasz aránya egyenlő a nagyobbik és az összegük arányával, akkor a két szakasz aránya ,,folytonos arány.'' (Az elnevezést az indokolja, hogy ‐ amint az könnyen látható ‐ a mondott tulajdonság öröklődik a hosszabbik szakaszból és a két szakasz összegéből álló párra.) Adott szakasz folytonos arányú részekre való osztását pedig ,,arany metszésnek'' nevezzük. Ez a tulajdonság könnyen ellenőrizhető a megoldásunkban kapott

(\sqrt[]{5} + 1)

2

szakaszhosszakra, és megoldásainkban azt is láttuk, hogy a

(\sqrt[]{5} + 1) : 2

arány az egyetlen folytonos arány.
3. A IV. megoldásban alkalmazott párhuzamos vetítést affinitásnak nevezik. Láttuk, hogy a vizsgált ötszögek mindig előállíthatók egy szabályos ötszög affin képeként, ezért ezeket az ötszögeket ,,affin szabályos ötszögnek'' is szokták nevezni.