Kezdőlap


Feladat:	1357. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Boruzs Mária , Mérő László
Füzet:	1971/szeptember, 19 - 21. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Síkgeometriai számítások trigonometriával, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1971/március: 1357. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás (szerkesztéssel). A feladat föltevései távolsági arányokat és egy szöget tartalmaznak, és a kérdés is szögre vonatkozik, így az alakzat tetszés szerint nagyítható.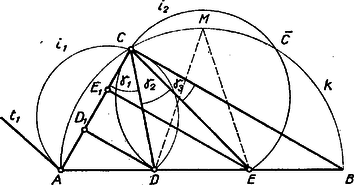
Fölvéve tetszőlegesen az $A B$ átfogót és kijelölve $D$ , $E$ harmadoló pontjait úgy, hogy $A D = D E = E B$ , a $C$ csúcs mértani helye egyrészt az $A B$ átmérőjű $k$ Thalész-félkör az $A B$ egyenessel kettévágott sík egyik, $F$ félsíkján, másrészt az $A D$ szakasz $A C D ∢ = γ_{1}$ nyílású $i_{1}$ látóköríve, és a $D E$ szakasz $D C E ∢ = γ_{2}$ nyílású $i_{2}$ látóköríve, ugyancsak az $F$ félsíkon ( $1$ . ábra, lásd a $20$ . oldalon).

1. ábra

1

. Ezek szerint ha

γ_{1}

adott, akkor

C

megfelelő helyzetét

k

-nak és

i_{1}

-nek az

A

-tól különböző közös pontja adja, és

γ_{2}

C D

C E

félegyenesek közti szög. A szerkesztés helyessége nyilvánvaló. Eljárásunk egyértelműen megadja

γ_{2}

-t, természetesen a nyilvánvaló

0^{\circ} < γ_{1} < 90^{\circ}

esetre szorítkozva, ekkor ugyanis

i_{1}

-nek

A

-beli

t_{1}

félérintője ‐ az érintőjének

F

-beli félegyenese tompaszöget

(180^{\circ} - γ_{1}

-et) zár be az

A B

félegyenessel, ezért

i_{1}

-nek van pontja

k

-n kívül,

D

végpontja viszont belül van a

k

-n.
Meggondolásunk és szerkesztésünk akkor is érvényes, ha

γ_{1}

-et úgy értelmezzük, hogy

D

B

-hez közelebbi harmadolópontja az átfogónak, így azonban más lesz

γ_{2}

értéke. Itt jegyezzük meg mindjárt, hogy

γ_{1}

határozta meg magának az

A B C

háromszögnek a hegyes szögeit is.
2. Ha pedig

γ_{2}

adott, akkor

C

-ként

k

és

i_{2}

közös pontjai jönnek tekintetbe, és

γ_{1}

C A

C D

félegyenesek közti szög lesz. A közös pontok száma

2

1

, ill.

0

aszerint, hogy

i_{2}

metszi vagy érinti

k

-t, ill. hogy minden pontja

k

belsejében van.

k

-nak és

i_{2}

-nek közös szimmetria tengelye az

A B

és

D E

szakaszok

f

közös felező merőlegese, így a mondott érintés csak

f

-nek

k

-n levő

M

pontjában lehetséges. Ezt felhasználva

k

és

i_{2}

közös pontjainak száma aszerint lesz

2

1

, ill.

0

, hogy

γ_{2}

kisebb, ill. egyenlő, ill. nagyobb, mint a

D M E ∢

, vagyis annak az egyenlő szárú háromszögnek a szárszöge, melyben az alap és a magasság aránya

(A B / 3) : (A B / 2) = 2 : 3

. Más szóval, aszerint, hogy

\begin{matrix} \frac{γ_{2}}{2} ⋛ arc tg \frac{1}{3} (= 0,322 radián = 18^{\circ} 26'), γ_{2} ⋛ 36^{\circ} 52' . \end{matrix}

(1)

Két közös pont,

C

és

\bar{C}

esetén a szimmetria alapján az

A \bar{C} D ∢

egyenlő a

B C E ∢

-gel. Mondhatjuk tehát azt is, hogy

C

-re szorítkozva

A C D ∢

és

B C E ∢

a feladat második részének

2

megoldása, továbbá e két megoldás egyenlő, ha

C

M

-ben adódik, végül nincs megoldás

γ_{1}

-re, ha

C

-re sincs megoldás.

Borusz Mária (Tata, Eötvös J. Gimn., II. o. t.)

Mérő László (Tatabánya, Árpád Gimn., II. o. t.)

Megjegyzések. 1. Könnyű utánaszámítani, hogy

γ_{2}

határszögét megadja a

3

4

5

egységnyi oldalú (derékszögű) háromszög legkisebbik szöge is.
2. Könnyen általánosíthatjuk a megoldást arra az esetre, ha

A C B

tetszőleges adott szög; az

(1)

föltétel módosulásának vizsgálatát az olvasóra hagyjuk.
3. Adott

γ_{1}

esetében célhoz vezet a következő szerkesztés is. A

C A

félegyenesre (ugyanazon oldalán) fölmérjük

γ_{1}

-et, új szára

C D

(

D

a szár egy tetszőleges pontja) és az

A C B

ismert szöget (

2

. ábra).

D

-n át párhuzamost húzunk

B C

-vel, ennek metszéspontja

C A

-val

D_{1}

, ekkor

D_{1}

-et

C

-ből

3 / 2

-szeresére nagyítva kapjuk

A

-t, ennek tükörképe

D

-re

E

, és ezzel megkaptuk a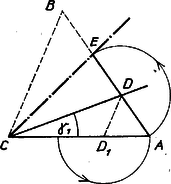

D C E

szöget.

2. ábra

II. megoldás (számítással). Legyen

D

és

E

merőleges vetülete

C A

-n

D_{1}

E_{1}

, így

C E_{1} = E_{1} D_{1} = C D_{1} / 2

és

E E_{1} = 2 D D_{1}

(

1

. ábra), tehát

\begin{matrix} tg γ_{1} = \frac{D D_{1}}{C D_{1}}, tg (γ_{1} + γ_{2}) = \frac{E E_{1}}{C E_{1}} = 4 tg γ_{1}, & (1) \\ tg γ_{2} = tg {(γ_{1} + γ_{2}) - γ_{1}} = \frac{tg (γ_{1} + γ_{2}) - tg γ_{1}}{1 + tg γ_{1} \cdot tg (γ_{1} + γ_{2})} = \frac{3 tg γ_{1}}{1 + 4 tg γ_{1}} . \end{matrix}

Adott

γ_{1}

‐ természetesen

0 < γ_{1} < 90^{\circ}

‐ esetén innen

tg γ_{2}

pozitív, és

γ_{2}

‐ mint hegyes szög ‐ egyértelműen meg van határozva.
Ha viszont

γ_{2}

adott, akkor átrendezéssel

\begin{matrix} 4 tg γ_{2} \cdot {tg}^{2} γ_{1} - 3 tg γ_{1} + tg γ_{2} = 0, & (2) \\ tg γ_{1} = \frac{3 \pm \sqrt[]{9 - 16 {tg}^{2} γ_{2}}}{8 tg γ_{2}}, \end{matrix}

valós megoldás létezésének föltétele

\begin{matrix} 9 - 16 {tg}^{2} γ_{2} \geq 0 azaz 0 < γ_{2} \leq arc tg \frac{3}{4}, \end{matrix}

(3)

és egyenlőség esetén

tg γ_{1}

két értéke egyenlő. Az egyenlőtlenség teljesülése esetén

(1)

-nek mindkét megoldása,

tg γ'_{1}

és

tg γ''_{1}

megfelel, mert pozitívok, hiszen

(2)

szerint összegük is, szorzatuk is pozitív:

\begin{matrix} tg γ_{1}' + tg γ''_{1} = \frac{3}{4 tg γ_{2}}, tg γ_{1}' \cdot tg γ_{1}'' = \frac{1}{4}; \end{matrix}

Azt is látjuk ezekből, hogy

γ'_{1} + γ''_{1}

γ_{2}

-nek pótszöge:

\begin{matrix} tg (γ'_{1} + γ''_{1}) = \frac{tg γ'_{1} + tg γ''_{1}}{1 - tg γ'_{1} \cdot tg γ''_{1}} = \frac{1}{tg γ_{2}} = ctg γ_{2}, \end{matrix}

tehát

γ'_{1} + γ_{2} + γ''_{1} = 90^{\circ}

, vagyis adott

γ_{2}

esetén

γ_{1}

-re ugyan két gyököt is kapunk, de ezek ugyanannak a háromszögnek rész-szögei.
Amennyiben az átfogó pontjainak sorrendje

A

E

D

B

, úgy

(1)

helyére

4 tg (γ_{1} - γ_{2}) = tg γ_{1}

lép,

tg γ_{2} = (3 tg γ_{1}) / (4 + {tg}^{2} γ_{1})

, ekkor

γ'_{1} + γ''_{1} - γ_{2} = 90^{\circ}

(

γ_{2}

kétszer fedett), a számítás hasonlóan végezhető, a valós megoldás létezésének föltétele ‐ a szimmetria alapján ‐ ismét

(3)

, csak egy megoldás van.

Megjegyzés. Könnyű belátni, hogy

B C E ∢ = γ_{3}

jelöléssel fennáll

3 sin γ_{1} \cdot sin γ_{3} - sin γ_{2} = 0

, ennek alapján is végezhetjük számításainkat, eleve tudva, hogy

γ_{1}

és

γ_{3}

a feladat

2

. részének

2

. megoldása.