Feladat: 1352. matematika gyakorlat Korcsoport: 14-15 Nehézségi fok: átlagos
Füzet: 1975/március, 114 - 117. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek szerkesztése, Alakzatok köré írt kör, Gyakorlat
Hivatkozás(ok):Feladatok: 1971/február: 1352. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A keresett ABC háromszögben az adott oldal szerepét AB= =c-nek adjuk, így az összegként adott hosszúság s=BC+CA=a+b lesz.

 

1. Kiindulunk egy kívánt r sugárral leírt k körből, legyen a középpontja O, megválasztjuk rajta az A csúcs helyzetét és ettől c távolságra kijelöljük k-n a B-t; így már csak C-t kell meghatároznunk.
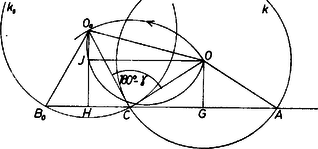
Most ‐ a feladatot megoldottnak tekintve ‐ fordítsuk rá B-t C körül AC meghosszabbítására, a B* helyzetbe (1. ábra, a betűk melletti indexeket csak később vegyük figyelembe, az AB egyenestől balra is, jobbra is egy-egy megfelelő háromszög látható).
 

 

1. ábra
 

Így egyrészt AB*=AC+CB=s, másrészt a CB*B háromszög egyenlő szárú, és C-nél levő külső szöge γ=ACB∢=12AOB∢. (Az utóbbi szögön a C-t nem tartalmazó AOB szögtartományt értjük, ami 180∘-nál nagyobb is lehet, ha ti. C a rövidebbik AB köríven van.) Eszerint CB*B∢=AB*B∢=γ2=14AOB∢, ismert.
Ezzel B*-ra két mértani helyet kaptunk: rajta van az A körüli, s sugarú k* körön, másrészt az AB szakasz γ2 nyílású i látszögkörívén, az AB egyenesnek C-t tartalmazó partján. A k* és i közös pontjaként kapott B*-ot A-val összekötő egyenes k-ból kimetszi C-t és ezzel a szerkesztést befejeztük.
 

2. A végrehajtásra térve, megjegyezzük, hogy az i körív D középpontjából AB látószöge 2⋅AB*B∢=γ=ACB∢, tehát D rajta van k-nak a C-t tartalmazó AB ívén, továbbá DA=DB miatt az AB oldal felező merőlegesén is; i tehát könnyen megrajzolható.
 

3. Bebizonyítjuk, hogy a kapott ABC háromszög megfelel a követelményeknek. Valóban, csúcsai egy r sugarú kör kerületén vannak; továbbá AB oldala egyenlő az előírt c-vel; végül a CB*B háromszög B*-nál levő szöge feleakkora, mint az ADB∢=ACB∢, ami e háromszög C-nél levő külső szöge; ezért ez a háromszög egyenlő szárú, tehát AC+CB=AC+CB*=AB*=s, amint a feladat kívánja.
4. Az A csúcs megválasztása után B létrejön, hacsak c≤2r; egyenlőség esetén a két AB félkör közül a szimmetria alapján bármelyiket választhatjuk D, majd C számára, és ha a háromszög a továbbiak szerint létrejön, akkor C-nél derékszögű lesz. * Ha viszont c<2r, akkor a szerkesztés folytatását egyaránt meg kell próbálnunk a nagyobbik AB ívnek D1 és a kisebbik AB ívnek D2 felezőpontjából kiindulva.
A Dj körüli, DjA=Rj sugarú ij körív (j=1,2) mindenesetre létrejön. Bj* -ot tekintve, eleve szükséges, hogy d>c legyen, másrészt k*-nak akkor és csak akkor van közös pontja ij-vel, ha még s≤2Rj, vagyis az AOF és ADjF derékszögű háromszögek (F felezi AB-t) felhasználásával
c<s≤2Rj=22r2±r4r2-c2,(1)
speciálisan c=2r esetén
2r<s≤22r.(1a)

Amennyiben s=2Rj, akkor egy közös Bj* pont van, Cj azonosnak adódik Dj-vel ‐ hiszen ekkor Bj* a k* és ij közös ADj tengelyén (átmérőegyenesén) van ‐, a kapott háromszögben CjA=CjB=s/2 (ilyen az 1. ábrán B2* esete). Ha viszont s<2Rj, akkor helyzet szerint két közös pontot kapunk (az 1. ábrán B1* és B1*'), a belőlük adódó két Cj pont azonban két egybevágó háromszögre vezet, tehát számunkra nem tekintendő külön megoldásnak. Valóban, ekkor Bj* és Bj*' egymás tükörképei ADj-re, így
C'jADj∢=Bj*'ADj∢=Bj*ADj∢=CjADj,C'jDj^=CjDj^
vagyis a két Cj pont ‐ és a két ABCj háromszög ‐ tükrös pár az ODj tengelyre.
Ezek szerint c<2r mellett a megoldások száma annyi, ahány j indexre teljesül (1), más szóval ahány ij ívvel van közös pontja k*-nak, ez a szám lehet 2, 1 vagy 0; c=2r mellett pedig 1 vagy 0 aszerint, hogy s-re teljesül-e (1a) vagy nem. (A két különböző AB íven kapott C pontok nem adhatnak egybevágó megoldásokat, hiszen C-nél levő szögük különböző.)
(Megjegyezzük, hogy az ABC háromszög adódhat egyenlő szárúnak úgy is, hogy a és b valamelyike ‐ vagy akár mind a kettő ‐ egyenlő c-vel. Ennek feltételét azonban nem keressük, a CA=CB esetet is csupán szemléletesség kedvéért említettük meg.)
 

Megjegyzések. 1. A fentiekben példát adtunk egy szerkesztési feladat ún. ,,klasszikus'' megoldásának 4 fő szakaszára:
1. Elemzés (kapcsolatok megállapítása az ismeretlen alakzat és az adatok között.
2. A szerkesztés végrehajtásának részletei.
3. Bizonyítása annak, hogy a szerkesztett alakzat megfelel az előírásoknak.
4. Diszkusszió: annak vizsgálata, hogy a szerkesztés az adatok közti milyen nagyságviszonyok (egyéb kapcsolatok) mellett végezhető el, és hogy esetenként hány megoldás van.
‐ Ezek a lépések természetesen a feladattól függően módosulhatnak, el is maradhatnak.
 

2. Régebbi tankönyvekben típusfeladatként szokott szerepelni a háromszögnek az a+b, c, γ adathármasból való szerkesztése. Tulajdonképpen ilyen az 1 alatt említett is, hiszen abban körről nincs szó, nincs kiemelve, hogy az átfogó egyszersmind a körülírt kör átmérője. Ezeket az eseteket is b-nek a meghosszabbítására való ráfordításával szokás megoldani, amint ezt az elemet mi is fölhasználtuk. A fenti megoldással szemben viszont eltérés, hogy ott a egyenesét és rajta az s szakaszt rögzítjük, egyik végpontjában hozzá γ/2 szöggel hajló félegyenest szerkesztünk és ezt elmetsszük a másik végpont körüli c sugarú körrel, tehát más sorrendben ,,vetjük be'' adatainkat.
Számos megoldás érkezett erre az esetre való visszavezetéssel. Ezekben nehézségként jelentkezik, hogy γ megszerkesztéséhez előre föl kell vennünk egy r sugarú kört, de nem ez lesz a végül kiadódó háromszög körülírt köre, és a föntivel szemben külön gond annak a bizonyítása, hogy a körülírt kör sugara valóban r. Az is gyakori az ilyen megoldásokban, hogy γ-ként csak a hegyesszöget veszik figyelembe ‐ különben a tompaszöget a fenti elv szerint is el lehet felejteni.
 

3. Felhívjuk az olvasó figyelmét a 107. oldalon közölt cikkünkre, amely ugyanennek a feladatnak térbeli ‐ ábrázoló geometriai ‐ meggondolásokon alapuló megoldását tartalmazza.
 

4. Az alábbi megoldásvázlat más érdekes kapcsolatokat használ, de a végrehajtás, a bizonyítás és a diszkusszió hosszadalmas. A teljes kidolgozást az olvasóra hagyjuk.
 

II. megoldás. (vázlat). Az 1. ábra CAO háromszögét próbáljuk megszerkeszteni. Fordítsuk el a CBO háromszöget és k-t C körül úgy, hogy B az AC oldal meghosszabbítására jusson, és jelöljük BO és k új helyzetét B0O0-lal (B0 azonos a fenti B*-gal).
 

 

2. ábra
 

Az elfordítás mértéke a C-nél levő külső szög: 180∘-γ, amekkora az AB látószöge D2-ből, ha C-t a D1 oldalán várjuk, illetve D1-ből, ha D2 oldalán. Eszerint a fönti k, A, B, Dj (j=1,2) rendszer fölvétele után megszerkeszthetjük egy új helyzetben az OCO0 egyenlő (r) szárú háromszöget, k-t és k0-t, és most olyan szelő szerkesztését tekintjük célunknak C-n át, melyre a k-ba és k0-ba eső húrok összege B0A=s.
Jelöljük az AC és CB0 szakasz felezőpontját G-vel, H-val és O vetületét az O0H egyenesen J-vel. Ekkor nyílván OJ=GH=s/2, ebből J az ismert OO0 szakasz fölötti Thalész-körön kijelölhető, és a kívánt szelő OJ-vel párhuzamos. A szelő CB0 szakaszát C körül (180∘-γ)-val visszafordítva kapjuk B-t.
Ekkor azt kell bizonyítanunk, hogy B ráesik k-ra és hogy BA=c.
A végrehajtást (180∘-γ) helyén γ-val meg kell ismételni.
 

Megjegyzés. Ennek a megoldásnak C a kulcspontja, de az ide előzetesen elhelyezendő (180∘-γ) szöghöz nem juthatunk hozzá A és B előbbi, ideiglenes ‐ később kárba vesző ‐ fölvétele nélkül. C tehát ,,nehéz'' pontja a feladatnak. (Így jól láthatjuk, hogy az I. megoldásban nincs fölösleges szerkesztési lépés, mindegyik adatunkat csak egyszer használtuk.)
*Ez a speciális eset a középiskolai I. o. tankönyv (1966. évi kiadás) 402. oldalának 33. feladata.