Feladat: 1350. matematika gyakorlat Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Császár Gyula ,  Kémeri Viktória ,  Oláh Vera 
Füzet: 1971/november, 141 - 144. oldal  PDF  |  MathML 
Témakör(ök): Számelrendezések, Kombinatorikus geometria síkban, Permutációk, Gyakorlat
Hivatkozás(ok):Feladatok: 1971/február: 1350. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Jelöljük a kis körökben elhelyezett számokat az ábra szerint, és a belső körben elhelyezett számok összegét S-se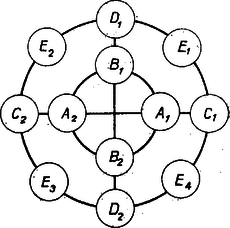l.

 

 

Feladatunk szerint olyan elhelyezéseket keresünk, amelyekre teljesül
A1+A2+B1+B2=S,(1)A1+A2+C1+C2=S,(2)B1+B2+D1+D2=S,(3)C1+C2+D1+D2+E1+E2+E3+E4=2S.(4)
Az (1) és (4) egyenletek bal oldalainak az összege az adott 12 szám összegével, 1+2+3+...+12=78-cal egyenlő, emiatt S+2S=78, és S=26.
Jelöljük az azonos nagy betűkkel jelölt számok összegét a megfelelő kis betűvel. Az (1) és (2) egyenletek különbsége szerint b=c, az (1) és (3) egyenletek különbsége szerint a=d. Tehát egy megfelelő elhelyezésre
a+b=26,a=d,b=c(5)
teljesül. Ez a feltétel viszont elégséges is ahhoz, hogy egy elhelyezés megfelelő legyen, hiszen belőle (1), (2) és (3) nyilvánvalóan következnek, (4) pedig azért, mert a bal oldalán álló számok összege a+b=26-tal kevesebb az adott 12 szám összegénél, vagyis ez az összeg 78-26=2⋅26. Azt fogjuk megszámolni, hány olyan elhelyezés van, amely eleget tesz (5)-nek.
Egy megfelelő elhelyezésben az azonos nagy betűkkel jelzett számok egymás között tetszőlegesen felcserélhetők, hiszen (5) csak e számok összegére jelent feltételt (ha egyáltalán jelent feltételt, az Ei számokra (5) ugyanis semmit sem követel meg). Minden megfelelő elhelyezésből az Ai, Bi, Ci, Di (i=1,2) számpárok felcserélésével 2⋅2⋅2⋅2=24 új, és továbbra is megfelelő elhelyezést kapunk, az E1, E2, E3, E4 számokat pedig 24-féleképpen rendezhetjük át. Ha ugyanis 4 különböző számot minden lehetséges sorrendben fel akarunk írni, akkor az első helyre kerülő számot 4-féleképpen választhatjuk meg közülük, a másodikat a visszamaradó 3 közül 3-féleképpen, a harmadikat 2-féleképpen, ezután a negyedik egyértelműen a még el nem helyezett szám lesz. A lehetőségek száma ezek szerint valóban 4⋅3⋅2=24. További két-két lehetőséget jelent, hogy az A1, A2 számpárt felcserélhetjük a D1, D2 számpárral, a B1, B2 párt pedig a C1, C2 számpárral.
Válasszuk meg például a számok elhelyezését úgy, hogy az azonos nagy betűvel jelzett számok között mindig a nagyobb indexű legyen nagyobb, továbbá teljesüljön még, hogy A1<D1, B1<C1. A mondott átrendezésekkel minden megfelelő elhelyezésből ilyen, ennek a kiegészítő feltételnek is eleget tevő elhelyezésre juthatunk; és minden, ennek a kiegészítő feltételnek is eleget tevő elhelyezésből 24⋅24⋅22=29⋅3 további, megfelelő elhelyezést kapunk. Ha tehát a kiegészítő feltétel mellett az elhelyezések száma k, akkor az összes megfelelő elhelyezés száma 29⋅3⋅k. Mivel az Árpád állításában szereplő 8768 egyenlő 26⋅137-tel, Árpád szerint k értéke 2⋅137=274. Látni fogjuk, hogy k értéke ennél valamivel kevesebb, Árpád valószínűleg k meghatározásánál követett el hibát.
II. Rátérünk k meghatározására, ezt a lehetséges értékei szerinti esetszétválasztással végezzük el. Mivel a-t kétféleképpen is elő kell tudnunk állítani különböző számaink összegeként, a legkisebb lehetséges értéke 5. Ekkor A1=1, A2=4, D1=2, D2=3 az egyetlen, a kiegészítő feltételnek is eleget tevő megoldás, és a Bi, Ci változók értéke is egyértelműen meghatározott.
Az a=6 esetben is két lehetséges felbontás van: 5+1 és 4+2, és csak két lehetséges felbontása van a b=20 számnak is, ismét 1 megoldás van. (a és b=26-a mindig ugyanannyiféleképpen állítható elő 2-2 különböző, az előírtak közül választott számból, hiszen ha a=x+y, akkor b=26-a=(13-x)+(13-y) és pl. x-szel együtt (13-x) is az előírt számok közé tartozik.)
Ha a=7, a felbontások: 6+1, 5+2, 4+3; a b=19 szám felbontásai pedig 12+7, 11+8, 10+9. Mivel a és b felbontásai közt csupa különböző számok lépnek fel, bárhogy választunk ki e 3-3 felbontás közül kettőt-kettőt, megfelelő elhelyezést kapunk, a lehetőségek száma tehát 3⋅3=9. (Három elem közül ugyanis 3-féleképpen választhatunk ki kettőt, hiszen a kiválasztást meghatározza, hogy melyiket nem választjuk ki, és erre 3 lehetőségünk van.)
Ha a=8, akkor 8=7+1=6+2=5+3 és b=18=12+6=11+7=10+8, de az a=1+7 felbontás mellé nem választhatjuk a b=7+11 felbontást és (2+6) mellé a (6+12)-t (táblázatunkon az egymást kizáró párokat vonallal kötöttük össze). Kell tehát, hogy a egyik felbontása (3+5), b egyik felbontása (8+10) legyen, ezek mellé a második felbontását 2-féleképpen választhatjuk és mindegyik esetben egyértelmű, hogy mi a b másik felbontása. A megoldások száma innen 2⋅1=2.
 

a=8:1+72+63+5||b=18:7+116+128+10a=9:1+82+73+64+5||||b=17:8+97+106+115+12

I.II.III.IV.a=10:1+93+74+62+8\//\b=16:9+74+126+105+11αααββa=11:1+105+62+93+84+7\/\//\/\b=15:5+106+93+127+84+11αααββa=12:1+113+95+72+104+8\/\//\/\b=14:3+115+92+124+106+8
 

Ha a=9, négy lehetséges felbontás van, ezek mindegyike a b=17 felbontásai közül egyet zár ki, amint táblázatunk mutatja. Bárhogy választunk ki tehát a négy lehetséges felbontása közül kettőt, b felbontásai közül csak az általuk ki nem zárt másik kettőt választhatjuk. A lehetőségek száma tehát annyi, ahányféleképpen a-nak 4 lehetséges felbontása közül kettőt kiválaszthatunk. A lehetőségek ‐ a felbontásokat I, II, III, IV-gyel jelölve: I‐II, I‐III, I‐IV, II‐III, II‐IV, III‐IV, tehát 6 lehetséges párosítás van.
a=10-nek is 4 felbontása van, ezek közül kettő (jelöljük őket I-gyel és II-vel) a b=16-nak ugyanazt a felbontását zárja ki, egy harmadik (jelöljük III-mal) két felbontást is kizár, egy (a IV) pedig nem zár ki egyet sem. A III mellé csak IV-et vehetjük párnak, ekkor b két felbontása egyértelmű; ha IV mellé I-et vagy II-t vesszük, vagy ha I-et II-vel párosítjuk, b-nek 3-féle felbontása közül választhatunk, a lehetőségek száma tehát összesen 1+3⋅3=10.
Ha a=11, két független lánc alakul ki az a és b egymást kizáró felbontásaiból, a felbontásai közül az egyikben 3 van (ezeket α-típusúaknak nevezzük), a másikban 2 (ezek a β-típusúak). Ha a mindkét felbontását az α-típusúak közül választjuk ki, ezekhez b-nek 3 felbontása közül választhatunk, és az ilyen lehetőségek száma 3⋅3=9. Egy α és egy β típusú felbontást választva a-hoz csak akkor kapunk megoldást, ha olyan α-típusút választunk, amelyik b-nek csak egy felbontását zárja ki; ekkor b megfelelő felbontása egyértelműen meghatározott. Így 2⋅2=4 esetet kapunk, végül 1 megoldást ad a két β-típust felbontás választása, ezek együtt 3⋅3+2⋅2+1=14 megfelelő felbontást jelentenek.
a=12 esetén ugyanígy két független és az előbbiekkel egyenlő szerkezetű lánc alakul ki, a megoldást adó felbontások száma itt is 14. Az a>13 eseteket rendre visszavezethetjük a már tárgyalt esetekre (a és b szerepének a felcserélésével), ezeket összefoglalva mutatja be az alábbi táblázat:
 


a     5  6  7  8  9  10  11  12(b)     21  20  19  18  17  16  15  14a megoldások száma    1  1  9  2  6  10  14  14  
 

Az eddigiek szerint az a≠13 értékekben összesen 2⋅57=114 megoldást találtunk.
Külön kell tárgyalnunk az a=b=13 esetet. Ekkor 6 megfelelő felbontás van, ezek közül először az a felbontásaihoz választunk ki kettőt, amit 5+4+3+2+1=15-féleképpen tehetünk meg (az egyes felbontásokat ismét római írású számokkal jelölve, I mellé a másik 5-öt választhatjuk, II mellé a többi 4-et ‐ hiszen a II‐I párt már számításba vettük ‐ és így tovább, végül V mellé egyedül a VI-ot választhatjuk). A többi 4-ből választhatjuk ki b két felbontását, amit (mint azt az a=9 esetnél láttuk) 6-féleképpen tehetünk meg; így az összes megoldás száma a=13 mellett 15⋅6=90, minden a értékre együtt k=90+114=204, és az elhelyezési lehetőségek száma 29⋅3⋅204=313344.
 

Megjegyzés. Többen avval vélték bizonyítani az állítás helytelen voltát, hogy a közölt eredmény 8768-as tényezőjében szereplő 137-es prímtényező nem adódhat ki kombinálási művelet eredményeként. Ez nem helyes megokolás. A fentiekben is láttuk, hogy kombinálási lehetőségek száma nem kizárólag szorzással adódhat ki. (Lásd e szám vezető cikkét is.)par