Kezdőlap


Feladat:	1346. matematika gyakorlat	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1973/február, 64 - 66. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Trapézok, Paralelogrammák, Vektorok lineáris kombinációi, Helyvektorok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1971/január: 1346. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a $C F$ , $D G$ (azaz $H G$ ) egyenesek metszéspontját $K$ -val, a trapéz szemben fekvő $A$ , $C$ és $B$ , $D$ csúcspárjait összekötő egyenesek metszéspontját $M$ -mel, továbbá legyen $A B = p$ és $D C = q$ . A $p = q$ esettel nem kell foglalkoznunk, mert $p = q$ mellett, és ha még az $A B C D = T$ trapéz konvex (azaz paralelogramma), az $F$ , $G$ és $H$ pontok mindegyike az $A$ csúcsban adódik, tehát az állítás semmitmondó; ha pedig $p = q$ és $T$ hurkolt (vagyis az $A B D C$ körüljárás adna paralelogrammát), akkor az $M$ metszéspont nem létezik. Az alakzatot konvex trapéz esetére az 1a és 1b ábrák, hurkolt trapéz esetére a 2a és 2b ábrák szemléltetik a $p > q$ , illetve $p < q$ nagyságviszony mellett. Az utóbbi megkülönböztetésre amiatt van szükség, mert az alakzat előállításában és a bizonyítandó állításban az $A$ , $B$ , $C$ , $D$ csúcsok mindegyike megkülönböztetett szerepet játszik (azaz $A$ és $D$ , valamint $B$ és $C$ nem ekvivalensek).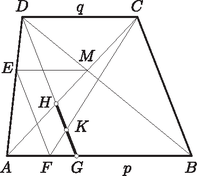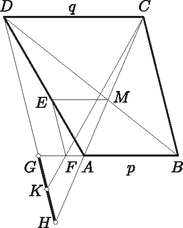

1a. ábra

1b. ábra

A szerkesztés szerint a

K G F

és

C B F

háromszögek minden esetben hasonlók egymáshoz, úgyszintén a

H G A

C B A

háromszögek is. Ezek alapján

\begin{matrix} H G : K G = (\frac{A G}{A B} \cdot C B) : (\frac{F G}{F B} \cdot C B) = \frac{A G}{F G} : \frac{A B}{F B}, \end{matrix}

(1)

és azt kell bizonyítanunk, hogy ennek az aránynak az értéke 2.
Mivel az

A B M

és

C D M

háromszögek hasonlók egymáshoz, azért

\begin{matrix} \frac{A F}{F G} = \frac{A E}{E D} = \frac{A M}{M C} = \frac{A B}{D C} = \frac{p}{q} . \end{matrix}

(2)

Konvex

T

esetében

M

A C

szakaszon van, ezért

E

A D

szakaszon,

F

A G

szakaszon, így

A G = A F + F G = | p - q |

, ezért (2) alapján

\begin{matrix} A F = \frac{p}{p + q} \cdot A G, F G = \frac{q}{p + q} \cdot A G, \end{matrix}

és (1) utolsó előtti tagja céljára

\begin{matrix} \frac{A G}{F G} = \frac{p + q}{q} . \end{matrix}

(3)

Másrészt a

p > q

, illetve

p < q

nagyságviszony szerint:

\begin{matrix} F B = B G \pm G F = q \pm \frac{q}{p + q} \cdot | p - q |, \end{matrix}

és mivel rendre

| p - q | = \pm (p - q)

, azért

F B

, majd (1) utolsó tagja, majd (3) figyelembevételével (1) értéke mindkét nagyságviszony esetére

\begin{matrix} F B = \frac{2 p q}{p + q}, \frac{A B}{F B} = \frac{p + q}{2 q}, \frac{H G}{k G} = 2. \end{matrix}

2a. ábra

2b. ábra

Hurkolt

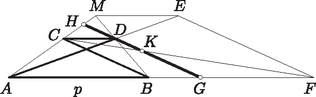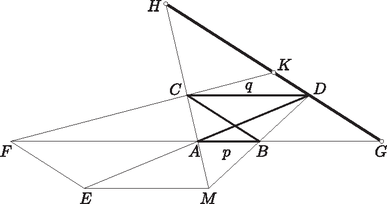T

esetében az

M

E

F

pont rendre az

A C

A D

A G

szakasz valamelyik meghosszabbításán van:

A G = | A F - F G |

, éspedig

p < q

esetén az

A

-n túli meghosszabbításon,

p > q

esetén a másikon. (2) alapján

\begin{matrix} A F = \frac{p}{| p - q |} A G, F G = \frac{q}{| p - q |} A G, \frac{A G}{F G} = \frac{| p - g |}{q} = \frac{\pm (p - q)}{q} \end{matrix}

aszerint, hogy

p ≷ q

. Másrészt

F B = F G \pm G B

, továbbá mindenképpen

A G = p + q

. így

\begin{matrix} F B = \frac{q (p + q)}{\pm (p - q)} \pm q = \frac{2 q p}{\pm (p - q)}, \end{matrix}

és ezekből a konvex

T

esetéhez hasonlóan

H G : K G = 2

.
Ezzel az állítást minden szóba jövő esetre bebizonyítottuk.

II. megoldás. Jelöljük az

\vec{A B}

vektor irányába mutató egységvektort

e

-vel, az

\vec{A B}

vektor hosszát

p

-vel:

\vec{A B} = p e

. Mivel a

\vec{D C}

vektor párhuzamos

\vec{A B}

-vel,

\vec{D C}

is skalárszorosa

e

-nek:

\vec{D C} = q e

. Ez a

q

negatív is lehet, ha ugyanis az

A B C D

négyszög hurkolt, akkor

\vec{A B}

és

\vec{D C}

ellentétes irányúak. Legyen még

\vec{A E} = x \cdot \vec{A D}

\vec{E M} = y e

, első lépésként ennek az

x

és

y

számnak az értékét határozzuk meg.
Jelöljük az

A C

B D

átlók metszéspontját

M

-mel. Mivel

M

rajta van az

A C

egyenesen,

\vec{A M} = \vec{A E} + \vec{E M}

\vec{A C} = \vec{A D} + \vec{D C}

-nek egy

u

skalárszorosa, azaz

\begin{matrix} \vec{A M} = u \cdot \vec{A C}, x \cdot \vec{A D} + y \cdot e = u \cdot \vec{A D} + u q e. \end{matrix}

A nem párhuzamos

e

és

\vec{A D}

vektorokkal minden vektort egyértelműen állíthatunk elő, tehát

u = x

, és

y = u q = q x

. Mivel másrészt

M

rajta van a

B D

egyenesen, azért a

\vec{B M}

\vec{B D} = \vec{B A} + \vec{A D} = \vec{A D} - \vec{A B}

-nak egy

v

skalárszorosa:

\begin{matrix} \vec{B M} = v \cdot \vec{B D}, azaz - p e + x \cdot \vec{A D} + y e = v \cdot \vec{A D} - v p e, \end{matrix}

amiből

v = x

és

y = p (1 - x)

következik. Tehát

\begin{matrix} x = \frac{p}{p + q}; y = \frac{p q}{p + q}, \end{matrix}

feltéve, hogy

p + q \neq 0

, különben ugyanis

A C | | B D

, és

M

nem jön létre. ‐ A szerkesztés szerint

E F | | D G | | B C

, emiatt

\begin{matrix} \vec{A G} & = \vec{A B} - \vec{D C} = (p = q) e, \\ \vec{A F} & = x \cdot \vec{A G} = \frac{p (p - q)}{p + q} e, \\ \vec{F G} & = (1 - x) \vec{A G} = \frac{q (p - q)}{p + q} e. \end{matrix}

Jelöljük a

H

-n átmenő,

A B

-vel párhuzamos egyenesnek

C F

-en és

C G

-n levő pontjait

J

-vel és

L

-lel, ekkor

\vec{H L}

azt a szerepet játssza a

(p - q)

és

q

alapokkal bíró

A G C D

trapézban, mint

\vec{E M} = y e

A B C D

-ben, így

\begin{matrix} \vec{H L} = \frac{(p - q) q}{(p - q) + q} e, \end{matrix}

és

\vec{A F} = x \cdot \vec{A G}

\vec{H J} = x \cdot \vec{H L}

miatt ebből

\begin{matrix} \vec{H J} = \frac{(p - q) q}{p + q} e = \vec{F G} \end{matrix}

következik. Tehát

F G J H

paralelogramma, és az

F J

átló felezi

G H

-t, amint azt bizonyítani kellett.