Feladat: 1334. matematika gyakorlat Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Bolla Mariann ,  Lánczi Katalin ,  Prőhle Péter 
Füzet: 1971/május, 210 - 212. oldal  PDF  |  MathML 
Témakör(ök): Egyéb sokszögek hasonlósága, Forgatva nyújtás, Rombuszok, Párhuzamos szelők tétele, Négyszögek szerkesztése, Gyakorlat
Hivatkozás(ok):Feladatok: 1970/november: 1334. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük az adott négyszög csúcsait A, B, C, D-vel, és legyen P az AB szakasz tetszőleges pontja. A P-n át AC-vel, illetve BD-vel párhuzamosan húzott egyenes metszi a BC, illetve AD szakaszt, jelöljük a metszéspontokat Q-val, ill. S-sel, a Q-n átmenő, BD-vel párhuzamos egyenes és a CD szakasz metszéspontját jelöljük R-rel (1. ábr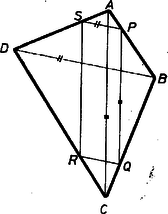a).

 
 
1. ábra
 

Megmutatjuk, hogy P, Q, R, S egy paralelogramma csúcsai.
Mivel a PS, QR oldalak a szerkesztés szerint párhuzamosak, elég azt megmutatnunk, hogy egyenlőek is. Az AC, PQ egyenesekre alkalmazva a párhuzamos szelők tételét:
AP:AB=CQ:CB.
A bal oldalon álló arány az ABD, APS háromszögek hasonlósága alapján egyenlő a PS:BD aránnyal, a jobb oldali pedig (a BCD és QCR háromszögek hasonlósága alapján) egyenlő a QR:BD aránnyal, tehát PS és QR valóban egyenlőek.
Kérdés mármost, hogyan kell a P pontot megválasztani, hogy PQRS rombusz legyen. Fenti megoldásunkhoz hasonlóan
PSPQ=BD⋅APAB:AC⋅PBAB=APPB:ACBD,
eszerint PS és PQ akkor és csakis akkor egyenlőek, ha
AP:PB=AC:BD,(1)
vagyis ha a P pont olyan szakaszokra bontja az AB szakaszt, melyek hosszának aránya egyenlő a négyszög átlóinak az arányával.
Ezt a P pontot többféleképpen megszerkeszthetjük. Mérjük fel például az A-n átmenő, BD-vel párhuzamos, az AC egyenes B-t tartalmazó oldala felé induló félegyenesre az AC szakaszt, és a kapott D1 pontot kössük össze D-vel. Ekkor a DD1 egyenes a keresett P pontban metszi az AB szakaszt, hiszen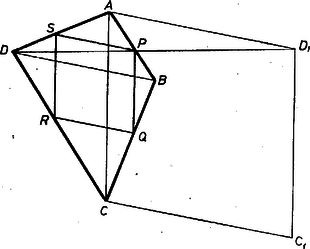
AP:PB=AD1:BD=AC:BD.
P-ból kiindulva a fent leírt lépésekkel kapjuk a követelménynek megfelelő rombuszt (2. ábra).
 
 
2. ábra
 

Lánczi Katalin (Budapest, Fazekas M. Gyak. Gimn., II. o. t.)

Prőhle Péter (Budapest, Fazekas M. Gyak. Gimn., I. o. t.)
 

Megjegyzések. 1. Azt mondtuk fentebb, hogy a P-n átmenő, AC-vel párhuzamos egyenes metszi a BC szakaszt. Valóban, az ABC háromszög AB oldalszakaszának tetszőleges pontján átmenő tetszőleges egyenes metszi a másik két oldalszakasz valamelyikét. A mi egyenesünk viszont nem metszheti az AC egyenest, hiszen párhuzamos vele, így metszenie kell a BC szakaszt.
2. Felhasználtuk, hogy az (1) összefüggés egyértelműen meghatározza a P pont, helyzetét. Valóban, ha P1 és P2 az AB szakasz különböző pontjai, és ‐ mondjuk ‐ P1 az AP2, szakaszon van, akkor AP1<AP2, P1B>P2B, tehát
AP1P1B<AP2P2B.
Eszerint legfeljebb egy pontra teljesülhet (1). Azt viszont láttuk, hogy van olyan pont, melyre (1) teljesül.
3. Meg lehet mutatni, hogy a beírt rombusz oldala feleakkora, mint a két átló harmonikus középarányosa. (Az a és b pozitív számok (szakaszok) harmonikus közepe h=2ab/(a+b).)
 

II. megoldás. Tegyük fel, hogy PQRS a keresett rombusz. Nagyítsuk ki ezt D-ből mint centrumból úgy, hogy S csúcsa A-ba kerüljön, ekkor R a C-be kerül, a P, Q csúcsok új helyzetét pedig jelöljük D1-gyel, C1-gyel. A kapott AD1C1C rombuszt megszerkeszthetjük, hiszen, AC oldala adott, AD1 oldala pedig párhuzamos a BD átlóval. Az így szerkesztett rombuszból D centrumú alkalmas kicsinyítéssel kapjuk a keresett rombuszt (2. ábra).
Szerkesztésünk helyességét nem bizonyítjuk, hiszen az ‐ mint könnyel látható ‐ lényegében azonos az I. megoldásban adott szerkesztéssel.
 

Megjegyzés. Noha a II. megoldásban ugyanazt a szerkesztést kaptuk, mint az I.-ben, e kettőt mégis különböző megoldásnak tekintjük, hiszen egy szerkesztési feladat megoldása nem csak a szerkesztés leírásából áll, hanem a szerkesztést előkészítő elemzésből, és a szerkesztés helyességének a bizonyításából. ‐ Előre felhívjuk az érdeklődők figyelmét a pontversenyen kívül közölt 80. probléma megoldására, melyben maga a szerkesztés egyetlen lépésből fog állni, a feladat megoldása viszont alapos megfontolást igényel.
 

III. megoldás (vázlat). A feladatot megfordítjuk: felveszünk tetszés szerint egy olyan P*Q*R*S* rombuszt, melynek oldalai párhuzamosak az adott ABCD=N négyszög AC, BD átlóival, ennek köréje írunk egy A*B*C*D*=N* négyszöget, melynek oldalai rendre párhuzamosak N egymás utáni oldalaival, végül az N*-nak és N-nek O hasonlósági középpontját a P*, Q*, R*, S* pontokkal összekötő egyenesek által N megfelelő oldalait metszve, kijelöljük a keresett PQRS rombusz csúcsait.
Avégett, hogy O az ábra belsejébe, N és N* közé essék, a felvett rombusz bal, alsó P* csúcsán át N-nek jobb, felső, AB oldalával húztunk párhuzamost, és így tovább (3. ábra).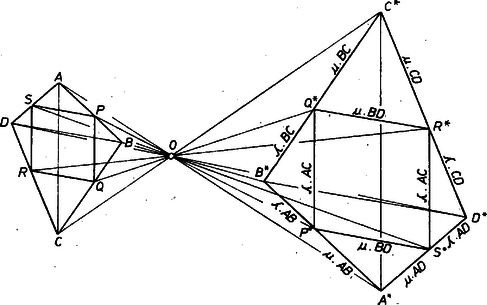
 
 
3. ábra
 

Itt természetesen bizonyítani kell, hogy N* hasonló N-hez, hiszen négyszögek esetében nem elég az egymás utáni szögek egyenlősége a hasonlósághoz. Hasonlók azonban az ACB és P*Q*B*, az ACD és S*R*D*, a BDA és P*S*A*, a BDC és Q*R*C* háromszögpárok, és P*Q*/AC=λ, P*S*/BD=μ jelöléssel N* oldalainak részei kifejezhetők N oldalaival (az ábrán bejegyezve). Ebből látható, hogy N* és N megfelelő oldalainak aránya λ+μ, így N* bármelyik részháromszöge hasonló N megfelelő részháromszögéhez, pl. A*B*C*▵∼ABC▵, tehát N*∼N, O létezik, eljárásunk helyes.
 

Bolla Mariann (Zirc, Gimn., II. o. t.)

dolgozata alapján, a bizonyítással kiegészítve.