Kezdőlap


Feladat:	1328. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Ábrahám Gy. , Baka I. , Bezdek K. , Boruzs Mária , Burda Magdolna , Csuzda I. , Horváth Gyöngyi , Horváth József , Horváth Mária , Izsák Éva , Kémeri Viktória , Keveházi A. , Kovács Julianna , Lakner P. , Makay L. , Németh M. , Oláh Vera , Pallagi D. , Párkány Katalin , Ruttkay Zsófia , Sándor T. , Somogyi Á. , Szabados Gy. , Szarvas G. , Szentpéteri J. , Szerényi T. , Tóth Erzsébet , Törő Ágnes , Vecsernyés P.
Füzet:	1972/január, 13 - 15. oldal		PDF \| MathML
Témakör(ök):	Középpontos tükrözés, Hossz, kerület, Szimmetrikus alakzatok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1970/október: 1328. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 3 alkalmas tükrözéssel elérjük, hogy a vizsgálandó háromszögeket külön‐külön látjuk. Tükrözzük először az eredeti $A B C$ háromszöget és ‐ az (1)-ben utolsó ‐ $A_{2} B_{1} C_{1}$ háromszöget a $B C$ oldal felezőpontjára, így $B$ és $C$ egymásba mennek át, $A_{2}$ képe $A_{1}$ lesz, és jelöljük $A$ , $B_{1}$ , $C_{1}$ képét rendre $A'$ -vel, $B''_{1}$ -vel, $C'_{1}$ -vel 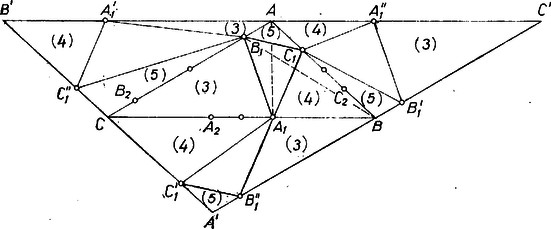(1. ábra).

1. ábra

Legyen hasonlóan az eredeti és az

A_{1} B_{2} C_{1}

háromszög tükörképe a

C A

oldal felezőpontjára

C B' A

A'_{1} B_{1} C''_{1}

, végül az eredeti és az

A_{1} B_{1} C_{2}

háromszög képe az

A B

oldal felezőpontjára

B A C'

, ill.

A''_{1} B'_{1} C_{1}

. Azt fogjuk bebizonyítani, hogy az

\begin{matrix} A_{1} B_{1} C_{1}, A_{1} B''_{1} C'_{1}, A'_{1} B_{1} C''_{1}, A''_{1} B'_{1} C_{1} \end{matrix}

(2)

háromszögek területének az összege egyenlő az

A B C

háromszög területével, ez nyilvánvalóan egyértelmű a feladat állításával. Azt mutatjuk meg, hogy ha a (2) háromszögeket kivágjuk az

A' B' C'

háromszögből, a visszamaradó részek összterülete egyenlő az

A B C

háromszög területének 3-szorosával. Állításunk ebből következik, hiszen az

A' B' C'

háromszög területe 4-szer akkora, mint az

A B C

háromszög területe.
Vizsgáljuk először a visszamaradó résznek azokat a háromszögeit, melyek

C

-re vagy ennek tükörképeire támaszkodnak, az

\begin{matrix} A_{1} B_{1} C A_{1} B B''_{1}, A A'_{1} B_{1}, A''_{1} C' B'_{1} \end{matrix}

(3)

háromszögeket. Mivel

B''_{1}

és

B_{1}

szimmetrikusak

B C

felezőpontjára, azért e két pont egyenlő távolságra van a

B C

egyenestől és az

A_{1} B B''_{1}

A_{1} B B_{1}

háromszögek területe egyenlő. Így a (3)-beli első két háromszög területének összege egyenlő a

B B_{1} C

háromszög területével. Ugyanígy kapjuk, hogy

A A'_{1} B_{1}

területe egyenlő

A A_{1} B_{1}

területével, az

A''_{1} C'_{1} B'_{1}

háromszög pedig egybevágó

A_{1} B_{1} C

-vel, tehát a (3)-beli utolsó két háromszög területének összege egyenlő az

A A_{1} C

területével.
Ugyanígy kapjuk, hogy a

B

-re vagy

B

valamelyik tükörképére támaszkodó

\begin{matrix} A_{1} B C_{1}, A_{1} C C'_{1}, A'_{1} B' C''_{1}, A''_{1} A C_{1} \end{matrix}

háromszögek területének összege egyenlő az

A A_{1} B

és

C C_{1} B

háromszögek területének összegével, és hogy az

A

-ra és tükörképeire támaszkodó

\begin{matrix} A B_{1} C_{1}, A' B''_{1} C'_{1}, B_{1} C C''_{1}, B B'_{1} C_{1} \end{matrix}

háromszögek területének összege egyenlő

B B_{1} A

és

C C_{1} A

területének összegével.
A kapott 6 háromszög viszont párokba állítható úgy, hogy páronként összeálljon belőlük az

A B C

háromszög:

A A_{1} C

és

A A_{1} B

B B_{1} A

és

B B_{1} C

C C_{1} A

és

C C_{1} B

. Állításunkat ezzel bebizonyítottuk.

II. megoldás. Azt fogjuk bizonyítani, hogy az

\begin{matrix} A_{1} B_{1} C_{2}, A_{1} B_{2} C_{1}, A_{2} B_{1} C_{1} \end{matrix}

háromszögek területének az összege egyenlő az

\begin{matrix} A B_{1} C_{1}, A_{1} B C_{1}, A_{1} B_{1} C \end{matrix}

háromszögek területének összegével. Ebből következik feladatunk állítása, mert az utóbbiak az

A_{1} B_{1} C_{1}

háromszöggel együtt kiadják az

A B C

háromszöget. Bizonyításunk során egy egyenesvonalú síkidom területét röviden úgy jelöljük, hogy felsoroljuk egymás utáni csúcsait, és ezeket zárójelbe tesszük. Ezzel a jelöléssel állításunk az

\begin{matrix} (A_{1} B_{1} C_{2}) + (A_{1} B_{2} C_{1}) + (A_{2} B_{1} C_{1}) = (A B_{1} C_{1}) + (A_{1} B C_{1}) + (A_{1} B_{1} C) \end{matrix}

(4)

egyenlőséget jelenti.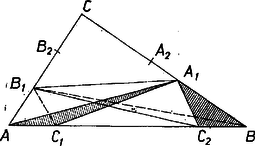

2. ábra

Egészítsük ki az

A_{1} B_{1} C_{2}

háromszöget

A_{1} B C_{2}

-vel négyszöggé, és ezt vágjuk ketté a másik átlójával (2. ábra):

\begin{matrix} (A_{1} B_{1} C_{2}) = (A_{1} B_{1} C_{2} B) - (A_{1} B C_{2}) = (A_{1} B B_{1}) + (B B_{1} C_{2}) - (A_{1} B C_{2}) . \end{matrix}

Itt az

A_{1} B C_{2}

háromszög területe egyenlő

A_{1} A C_{1}

területével, mert

A_{1}

csúcsuk és az ezzel szemközti oldaluk egyenese közös, továbbá az

A_{1}

-gyel szemközti oldaluk hossza is egyenlő, hiszen a

B C_{2}

szakaszt az

A B

szakasz felezőpontjára tükrözve

A C_{1}

-et kapjuk. Ugyanígy bizonyítható, hogy

(B B_{1} C_{2}) = (A B_{1} C_{1})

, tehát

\begin{matrix} (A_{1} B_{1} C_{2}) = (A_{1} B B_{1}) + (A B_{1} C_{1}) - (A A_{1} C_{1}) . \end{matrix}

(Kiküszöböltük a 2-es indexeket.) Az (1) bal oldalán álló másik két terület ugyanígy alakítható át:

\begin{matrix} (A_{1} B_{2} C_{1}) = (A A_{1} C_{1}) + (A_{1} B_{1} C) - (B_{1} C C_{1}), \\ (A_{2} B_{1} C_{1}) = (B_{1} C C_{1}) + (A_{1} B C_{1}) - (A_{1} B B_{1}) . \end{matrix}

Ezt a három egyenlőséget összeadva a bizonyítandó (4) egyenlőséget kapjuk, állításunkat ezzel bebizonyítottuk.