Kezdőlap


Feladat:	1326. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Torma Tamás
Füzet:	1971/április, 166 - 168. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1970/október: 1326. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Legyen a végrehajtott felbontás háromszögeinek száma $h$ , így oldalainak száma $3 h$ (az átlókat mindkét oldalukon levő háromszögekben számítva), és a bennük levő szögek összege $h \cdot 180^{\circ}$ . Minden ilyen szög azonos vagy a felbontandó sokszög valamelyik szögével ‐ ti. akkor, ha ennek a szögnek a csúcsából egyetlen átlót sem húztunk meg ‐, vagy pedig a sokszög egy szögének egy részével, mert minden háromszög csúcsai a sokszög csúcsai közül valók, hiszen a berajzolt átlók belső pontjaiban nem keletkezhetnek új csúcsok. Így $h \cdot 180^{\circ}$ egyenlő a sokszög $(n - 2)$ $180^{\circ}$ -nyi szögösszegével, ahol $n$ a sokszög oldalainak száma, ebből $h = n - 2$ , esetünkben $h = 10$ , a megrajzolandó átlók száma pedig $(3 h - 12) : 2 = 9$ , ugyanis a felbontó átlók 2‐2 háromszöghöz tartoznak hozzá, a sokszög oldalai pedig csak 1‐1 háromszöghöz.
Az előttünk álló $S z_{12}$ szabályos tizenkétszögnek $5$ -féle átlója van, ti. olyanok, amelyekkel a két partjukra jutó $12 - 2 = 10$ csúcs közül az egyik parton $1$ , $2$ , $3$ , $4$ , illetve $5$ csúcs van; mondjuk rendre $d_{1}$ , $d_{2}$ , $d_{3}$ , $d_{4}$ , $d_{5}$ típusúnak az ilyen átlókat. $d_{1}$ típusú átló legalább $2$ lép föl bármely $n (\geq 5)$ oldalú sokszög háromszögekre való felbontásában, mert a sokszög $n$ oldala legföljebb $n - 2$ háromszög között oszlik el, és ha egy háromszögbe két sokszögoldal tartozik, egyik végpontjuk szükségképpen közös, tehát a háromszög vele szemben levő oldala $d_{1}$ típusú átló.
Nem fordulhat elő viszont az előírt típusú felbontásban $d_{2}$ típusú átló, mert az ilyen által lemetszett négyszöget még tovább kellene bontanunk valamelyik ‐ de csak az egyik ‐ átlójával, és ezek bármelyikét megrajzolva, a $d_{2}$ egyik partjára esett $2$ csúcs egyike $2$ , azaz páros számú háromszögbe tartoznék bele, a követelménnyel ellentétben.
Megmutatjuk, hogy nem rajzolhatunk be $d_{5}$ típusú átlót sem. Egy ilyen az $S z_{12}$ -t két hétszögre vágja, legyen egy ilyen $A B C D E F G$ , ahol $A G$ a $d_{5}$ típusú átló ( $1$ . ábra). Az ezt oldalként tartalmazó háromszög harmadik csúcsa nem lehet $D$ , mert az $A D$ átló $d_{2}$ típusú, így (a szimmetria alapján) elég $B$ -t és $C$ -t próbálni harmadik csúcsként.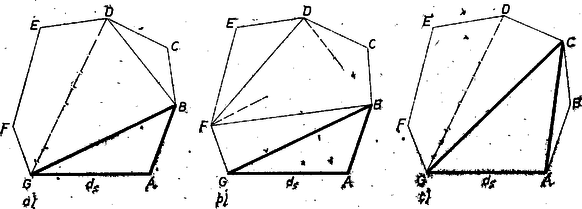

1. ábra

B A G

egy háromszöge a felbontásnak, akkor

B

-ből még vagy

1

vagy

3

átló húzandó meg ‐ hiszen a követelmény így is kimondható: amelyik csúcsból indul átló, onnan páros számú átlónak kell indulnia. Ámde

3

további átló nem húzható, mert köztük lenne

B E

, így csak

B D

-re és

B F

-re gondolhatunk (

1

. ábra a) és b) része). Az előbbi kényszerítően maga után vonná a kizárt

G D

-t, az utóbbi pedig

F D

-t, és ekkor a

B C D F

négyszög egyik átlójával sem bontható.
Ha pedig a

C A G

háromszög oldalává tesszük meg

A G

-t (1. c) ábra), evvel

C

-ből már

2

átló indul ki, többet

C F

miatt nem húzhatunk, ekkor pedig a kizárt

D G

-re kényszerülnénk. Így valóban nem húzható

d_{5}

típusú átló.
A

d_{4}

átlók hatszöget metszenek le, egy ilyenben (

2

. ábra

A B C D E F

, a lemetsző átló

A F

) a hétszög fenti esetéhez hasonlóan elég a

B A F

háromszöggel indulnunk.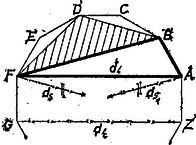

2. ábra

B

-ből csak

D

-be, onnan pedig csak

F

-be mehet a második átló, ekkor a

B

C

D

E

csúcsok rendre

3

1

3

1

háromszöghöz tartoznak, ez tehát megfelelő felbontás, a csatlakozó

A

F

csúcsokból pedig eddig páratlan számú átló indul ki.
Látni fogjuk, hogy

d_{3}

típusú átlók is használhatók lesznek. Könnyen adódik a lemetszett csúcsok, valamint a lemetsző átlók végpontjainál felhasznált csúcsok számából, hogy

d_{4}

-ből legföljebb

2

-t rajzolhatunk,

d_{3}

-ból

3

-at,

d_{1}

-ből pedig

6

-ot.

II. Ezek alapján rátérve a próbálgatásokra,

2

d_{4}

-es átló nem állhat külön végpontokkal (más szóval párhuzamosan,

2

. ábra,

A F

és

Z G

), mert a köztük keletkező négyszög mindkét átlója

d_{5}

típusú (másképpen:

A

-ból is,

F

-ből is kellene indítani átlót, hogy számuk párossá váljék). Ha viszont a

2

d_{4}

átló egyik végpontja közös, akkor nem közös végpontjaikat

d_{1}

átló köti össze, így a

3

végpontjuk mindegyikéből eddig 2‐2 átló indul ki, és a

d_{4}

-eseken kívül keletkező két hatszögbe ‐ most már az

S z_{12}

szimmetriát is tekintetbe véve ‐

3

lényegesen különböző módon másolhatjuk be a

2

. ábra hatszögének (egyetlen lehetséges) felbontását (3. ábra a), b), c) része).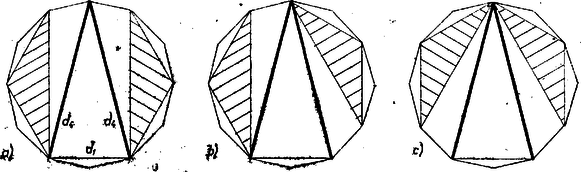

3. ábra

A

szerepére először mindkettőben a

2

d_{4}

-es átló közös csúcsát véve, majd e szerepet az egyik hatszögben, végül mindkettőben a

d_{4}

-es átló nem-közös végpontjának átadva. Ezzel

3

különböző megoldását kaptuk feladatunknak.
Nem lehetséges olyan felbontás, melyben csak

1

d_{4}

-es átlót engedünk meg, mert a másik oldalán keletkező nyolcszögben (

4

. ábra) az

A H

-t tartalmazó háromszög harmadik csúcsa

B

C

D

egyike sem lehet

H B = d_{5}

H C = d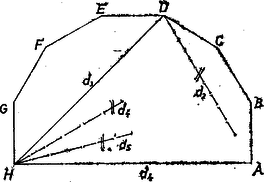_{4}

és

A D = d_{2}

miatt.

4. ábra

d_{4}

-es átló nélküli felbontásban a

9

berajzolandó átló céljára igénybe kell vennünk a fönt látott legnagyobb számokat, és a

3

d_{3}

-as,

6

d_{1}

-es átló csak egyféleképpen rajzolható be (

5

. ábra). ‐ Mindezek szerint a kívánt felbontások száma

4

5. ábra

Torma Tamás (Székesfehérvár, Petőfi S. Ált. Isk. 8. o. t.) dolgozata alapján, néhány kiegészítéssel

Megjegyzés. Az

1174

. gyakorlatban^{$^{*}$} a szabályos

9

szögről bizonyítottuk, hogy ugyanezen követelmény szerint csak egyféleképpen háromszögelhető.
Az

1967

. évi Kürschák-verseny

2

. feladata annak bizonyítása volt,^{$^{*}$} hogy csúcsonként páratlan számú háromszöget tartalmazva azok a konvex sokszögek háromszögelhetők, amelyek oldalainak száma osztható

3

-mal.

^{$^{*}$}K. M. L.

37

(1968)

12

. o.

^{$^{*}$}Hajós György: Az $1967.$ évi Kürschák József matematikai tanulóverseny feladatainak megoldása. K. M. L. $36$ $(1968)$ 193‐202. o. élesebben 194.‐197. o.