Kezdőlap


Feladat:	1323. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1971/február, 70 - 71. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Egyéb sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1970/szeptember: 1323. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a három átló felezőpontjait: ezek vagy különbözőek, vagy kettő azonos közülük. (Mindhárom nem lehet azonos, hiszen ekkor a három átló egy ponton menne át, és nem határoznának meg háromszöget.) Az alábbiakban megvizsgáljuk mind a két esetet.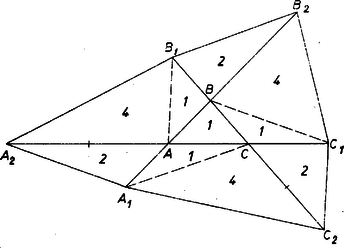
$a)$ Ha az átlók felezőpontjai különbözőek, akkor két átló metszéspontja az egyik átlót felezi, a másikat negyedeli. Jelöljük az átlók által meghatározott háromszög egyik csúcsát $A$ -val, az $A$ -n átmenő átlók közül $A_{1}$ és $B_{2}$ legyen annak a két végpontja, amelyet $A$ negyedel, ennek a felezőpontját jelöljük $B$ -vel ( $A$ az $A_{1} B$ szakaszt felezi, 1. ábra).

1. ábra

A

-n átmenő másik átló végpontjait jelöljük

A_{2}

-vel,

C_{1}

-gyel,

A

felezi az

A_{2} C_{1}

szakaszt, és legyen az

A C_{1}

szakasz felezőpontja a háromszög harmadik csúcsa, ezt jelöljük

C

-vel. A harmadik átló felezőpontja csak

C

lehet, és ennek

B

negyedelő pontja, a végpontok legyenek

B_{1}

és

C_{2}

(

B

B_{1} C

szakaszt felezi).
Válasszuk területegységnek az

A B C

háromszög területét. Az

A B C

A A_{1} C

háromszögek

C

csúcsa közös, a szemközti oldalak ugyanazon az egyenesen vannak és egyenlőek, tehát

A A_{1} C

területe is

1

. Hasonlóan

1

B B_{1} A

C C_{1} B

háromszögek területe is. Az

A C A_{1}

A_{2} A A_{1}

háromszögek

A_{1}

csúcsa közös, az ezzel szemközti oldalak ugyanazon az egyenesen vannak, és

A_{2} A = 2 A C

, tehát

A_{2} A A_{1}

területe

2

. Hasonlóan

2

B_{2} B B_{1}

C_{2} C C_{1}

háromszögek területe is.
Az

A_{1} B C

A_{1} C C_{2}

háromszögek

A_{1}

csúcsa közös, az ezzel szemközti oldalak ugyanazon az egyenesen vannak, és

C C_{2} = 2 B C

. Az

A_{1} B C

háromszög területe

2

, mert az

A C

súlyvonal két darab egységnyi területű háromszögre vágja, tehát

A_{1} C C_{2}

területe

4

. Hasonlóan

4

B_{1} A A_{2}

C_{1} B B_{2}

háromszögek területe is.
Az eredeti hatszög területe ezek szerint ebben az esetben

1 + 3 (1 + 2 + 4) = 22

-szerese az

A B C

háromszög területének.

b)

A második esetben legyen

C

az átlók által közbezárt háromszögnek az a csúcsa, amelyik a rajta átmenő mindkét átlót felezi, a harmadik átló felezőpontja legyen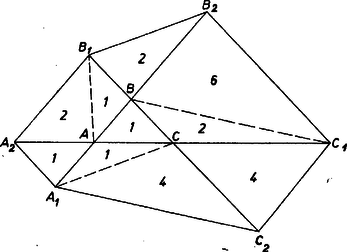

B

(2. ábra).

2. ábra

A B

B C

C A

oldalak legyenek rendre az

A_{1} B_{2}

B_{1} C_{2}

C_{1} A_{2}

átlón, és az

A B C

háromszög területe legyen ismét egységnyi.
A fentiekhez hasonlóan kapjuk, hogy az

A A_{1} C

B B_{1} A

C C_{1} B

háromszögek területe rendre

1

1

2

; az

A A_{1} A_{2}

B B_{1} B_{2}

C C_{1} C_{2}

háromszögeké

1

2

4

; az

A_{1} C C_{2}

B_{1} A A_{2}

C_{1} B B

háromszögeké pedig

4

2

6

. A hatszög területe tehát

24

-szerese az

A B C

háromszög területének.
Azt kaptuk tehát, hogy a feltett kérdésre nem egyértelmű a válasz, a hatszög területe vagy

22

-szerese vagy

24

-szerese az átlók által közbezárt háromszög területének aszerint, hogy a háromszög mindegyik csúcsa felezőpontja-e valamelyik átlónak vagy sem.