Feladat: 1322. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1971/február, 68 - 70. oldal  PDF  |  MathML 
Témakör(ök): Párhuzamos szelők tétele, Síkgeometriai számítások trigonometria nélkül háromszögekben, Síkgeometriai számítások trigonometria nélkül körökben, Gyakorlat
Hivatkozás(ok):Feladatok: 1970/szeptember: 1322. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a C, D pontokkal átellenes pontokat a körben C'-vel, D'-vel, és legyen AD', BC' metszéspontja N (1. ábr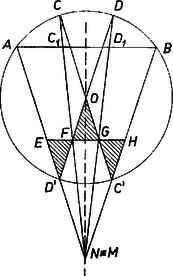a).

 
 
1. ábra
 

Mivel AC=CD=D'C', és A és D' a CC' átmérőnek ugyanazon az oldalán van, azért AD'∥CC'. Hasonlóan BC'∥DD', és az ANB, COD szögek egyállásúak, tehát egyenlők, tehát az ANB szög 1/3 akkora, mint az AOB szög. Azt fogjuk megmutatni, hogy N azonos M-mel ‐ ezzel igazoljuk a feladat állítását.
Szerkesztésünk szerint a CD, AB, C'D' egyenesek párhuzamosak, és a kapott alakzat szimmetria tengelye az ON egyenes. A COND' négyszög szemközti oldalai párhuzamosak ‐ hiszen CDC'D' téglalap, CD' párhuzamos az ON tengellyel ‐, tehát ez a négyszög paralelogramma, és CN felezi OD'-t. Jelöljük metszéspontjukat F-fel, DN és OC' metszéspontját G-vel. Láttuk, hogy F felezi OD'-t, hasonlóan láthatjuk be, hogy G felezi OC'-t, tehát FG párhuzamos D'C'-vel. F-re tükrözve O képe D', az OC' egyenes képe a vele párhuzamos D'A egyenes, ezen van G képe is, jelöljük ezt E-vel. Hasonlóan látható be, hogy F-nek G-re vonatkozó tükörképe, a H pont, a BC' egyenesen van. Ezek szerint F és G harmadolja az EH szakaszt, és EH∥AB. Tehát a CN, DN egyenesek harmadolják az AB szakaszt, vagyis azt a C1, D1 pontban metszik. Így a CC1, DD1 egyenesek M metszéspontja valóban azonos N-nel, feladatunk állítását bebizonyítottuk.
 

Megjegyzés. Az állítás akkor is érvényes, ha C és D a kör nagyobbik AB ívét harmadolják, ekkor természetesen a C, D pontokat tartalmazó, 180∘-nál nagyobb AOB szögre vonatkozik az állítás (2. ábra).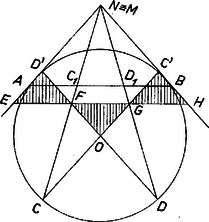
 
 
2. ábra
 

Ha ilyen esetben AOB∢=270∘, akkor C' a B-ben, D' az A-ban adódik, és AD' egyenesként a kör A-beli érintője értendő, BC'-ként a B-beli érintő. Érdekes speciális eset az is, ha A és B egy átmérő végpontjai.
 

II. megoldás. Húzzunk párhuzamost CO-val A-n át, DO-val B-n át, legyen ezeknek a metszéspontja N (3. és 4. ábr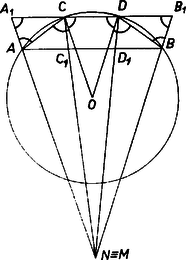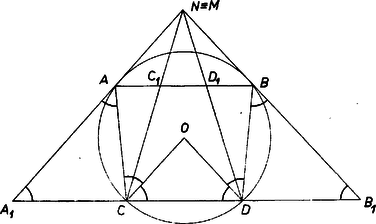a).
 
 
3. ábra
 
 
4. ábra
 

Ekkor az ANB, COD szögek egyenlőek, vagyis az ANB szög egyenlő az AOB szög harmadával. Azt fogjuk megmutatni, hogy N azonos M-mel, ezzel bebizonyítjuk feladatunk állítását.
Messe a CD egyenest AN az A1-ben, BN a B1-ben. Az AA1C, OCD szögek egyállásúak, A1AC, ACO pedig váltószögek, ezek a szögpárok tehát rendre egyenlőek egymással. CO felezi az ACD szöget, így az ACO, OCD szögek is egyenlőek, és egyenlőek az előbbi párjaik is, az AA1C háromszög AA1 oldalán levő szögek. AA1C tehát egyenlő szárú háromszög, A1C=AC.
Hasonlóan B1D=BD, és mivel AC=BD, ezekből következik, hogy A1C=CD=DB1, vagyis C és D harmadolja az A1B1 szakaszt. Mivel még A1B1∥AB, ebből következik, hogy a CN, DN egyenesek is harmadolják az AB szakaszt, N tehát valóban azonos M-mel, amint azt bizonyítani akartuk.