Kezdőlap


Feladat:	1310. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Angyal J. , Balog J. , Balogh Z. , Boros E. , Császár Gy. , Frey G. , Füredi Z. , Gáspár Gy. , Golda J. , Hanák G. , Hosszú F. , Huszár Magdolna , Kacsuk P. , Katona E. , Kirchner I. , Kiss Ipoly , Koppány I. , Kovács I. , Kuhár J. , Móri Tamás , Oláh Vera , Pallagi D. , Párkány Katalin , Petz D. , Prácser P. , Szendrei Ágnes , Szendrei Mária , Szeredi J. , Umáthum J. , Zárboch Zs.
Füzet:	1971/február, 64 - 66. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Súlyvonal, Magasságvonal, Súlypont, Magasságpont, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1970/április: 1310. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a keresett háromszög csúcsait $A$ , $B$ , $C$ betűkkel úgy, hogy ha még az $A$ -ból induló magasságvonal talppontja a $B C$ oldalegyenesen $A'$ , a $B C$ oldal felezőpontja $D$ , akkor az $A' A D$ szög egyenlő az első adott $δ$ szöggel, továbbá hasonlóan a $B' B E$ szög egyenlő a másik adott szöggel, $ε$ -nal, végül a háromszög $M$ magasságpontjának és $S$ súlypontjának távolsága egyenlő az adott $g$ hosszúsággal.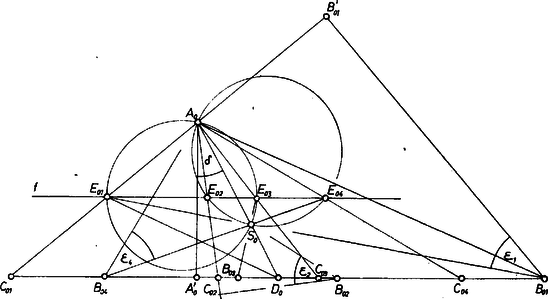
Az egyetlen lineáris adatot, $g$ -t egyelőre figyelmen kívül hagyva $δ$ -ból és $ε$ -ból az alábbiak szerint a keresetthez hasonló $A_{0} B_{0} C_{0}$ háromszöget szerkesztünk, végül ezt úgy nagyítjuk (kicsinyítjük), hogy a benne adódó $M_{0} S_{0}$ távolság megfelelője $g$ legyen. ‐ Az adott szögek természetesen hegyesszögek, vagy értékük $0$ ; az utóbbi lehetőségre majd csak a $δ$ , $ε > 0$ eset lezárása után térünk rá.
Az $A_{0} A'_{0}$ magasság megválasztása után a $δ$ hegyesszöggel szerkesztett $A_{0} D_{0} A'_{0}$ derékszögű háromszögből indulunk ki és kijelöljük ennek $A_{0} D_{0}$ átfogóján a harmadoló $S_{0}$ súlypontot $(A_{0} S_{0} = 2 S_{0} D_{0})$ . Ekkor az $A_{0} S_{0}$ szakasz látószöge az $A_{0} C_{0}$ oldal $E_{0}$ felezőpontjából vagy az adott $ε$ -nak a pótszöge, $90^{\circ} - ε$ ‐ti. az olyan háromszögekben, amelyekben a $B'_{0}$ magasságtalppont az $E_{0} A_{0}$ félegyenesen van, más szóval: ha $B_{0} A_{0} < B_{0} C_{0}$ ‐, vagy e pótszög kiegészítő szöge, $90^{\circ} + ε$ , ha ti. $B_{0} A_{0} > B_{0} C_{0}$ . Ezek szerint $E_{0}$ mértani helye annak a két teljes körnek a kerülete, amelyeknek pontjaiból az $A_{0} S_{0}$ szakasz $90^{\circ} - ε$ vagy $90^{\circ} + ε$ szögben látható ‐ természetesen $A_{0}$ -t és $S_{0}$ -t kivéve (1. ábra).

1. ábra

E_{0}

másik mértani helye pedig nyilvánvalóan az

A_{0} A'_{0}

magasságszakasz

f

felező merőlegese. A két mértani helynek

4

közös pontja van, mert

A_{0}

és

S_{0}

f

-nek két különböző partján van, és így

f

mindegyik kört

2

különböző pontban metszi és a

4

metszéspont is különböző, mert a két körnek csak

A_{0}

és

S_{0}

közös pontjai.
A

4

metszéspont bármelyikét véve

E_{0}

szerepére,

B_{0}

-t az

E_{0} S_{0}

egyenes,

C_{0}

-t pedig az

E_{0} A_{0}

egyenes metszi ki az

A'_{0} D_{0} = a_{0}

egyenesből. Mindegyik így kapott háromszög megfelel a követelményeknek, mert

E_{0}

felezi

A_{0} C_{0}

-t, hiszen

a_{0} ∥ f

, másrészt

S_{0}

harmadolja

E_{0} B_{0}

-t, mert

S_{0}

-nak

a_{0}

-tól való távolsága

A_{0} A'_{0} / 3

, tehát

f_{0}

-tól való távolsága

A_{0} A'_{0} / 2 - A_{0} A'_{0} / 3 = A_{0} A'_{0} / 6

, fele amannak; továbbá az

E_{0} B_{0} = E_{0} S_{0}

egyenes az

A_{0} C_{0}

egyenessel

90^{\circ} - ε

és

90^{\circ} + ε

szögeket zár be és így

A_{0} C_{0}

felező merőlegeséhez

ε

szöggel hajlik, tehát a vele párhuzamos

B_{0} B'_{0}

-höz is. Csak azt kell még belátnunk, hogy

A_{0} D_{0}

valóban súlyvonal, vagyis hogy a külön-külön kapott

B_{0}

és

C_{0}

D_{0}

-ra tükrös pontpár. Ez abból adódik, hogy

S_{0} E_{0} : S_{0} B_{0} = S_{0} D_{0} : S_{0} A_{0} = 1 : 2

alapján

A_{0} B_{0} ∥ E_{0} D_{0}

, így pedig

B_{0} C_{0} : B_{0} D_{0} = A_{0} C_{0} : A_{0} E_{0} = 2 : 1.

Akkor is érvényes meggondolásunk, ha az adott szögek egyike, mondjuk

δ = 0^{\circ}

; ekkor a háromszög nyilvánvalóan egyenlő szárú,

A_{0} B_{0} = A_{0} C_{0}

, és

a_{0}

-ként az

A'_{0}

-ben

A_{0} A'_{0}

-re állított merőleges veendő. Mivel ekkor a két kör egymás tükörképe

A_{0} A'_{0}

-re, a

4

megoldás is páronként egymás képe, tehát csak

2

különböző háromszöget kapunk. (Ha pedig az

ε > 0^{\circ}

szögből indulunk ki, akkor

(δ = 0^{\circ}

miatt a két kör egybeesik, Thalész-körré válik.)
Ha végül

δ = ε = 0^{\circ}

, akkor ezzel a háromszögnek

2

különböző szimmetriatengelyéről tudunk, tehát a háromszög szabályos. Ilyenkor nyilvánvalóan csak

g = 0

esetén van megoldás, és minden szabályos háromszög megfelel.
Könnyű belátni, hogy ha

δ = ε > 0

, akkor az egyik látókör középpontja

A_{0} A'_{0}

-n van, azonban az ábra mégsem szimmetrikus, megvan mind a

4

megoldás, közülük

2

egyenlő szárú.
Az előrebocsátott nagyításról csak azt kell megjegyezni, hogy a szerkeszthetőség feltétele ez:

g = 0

akkor és csak akkor álljon fenn, ha

δ = ε = 0

. Ezzel a feladatot megoldottuk.

Móri Tamás (Budapest, Berzsenyi D. Gimn., II. o. t. )

II. megoldás. Az I. megoldásban mondott, a keresetthez hasonló

A^{*} B^{*} C^{*}

háromszög szerkesztését kezdhetjük az

A^{*} B^{*}

oldal tetszés szerinti fölvételével is, valamint az ezáltal létrejött félsíkok közül annak a megválasztásával, amelyiken

C^{*}

-ot szerkeszteni kívánjuk (2. ábra).

2. ábra

A fentiekhez hasonlóan

A^{*} B^{*}

-nak

E^{*}

-ból vett látószöge

90^{\circ} - ε

vagy

90^{\circ} + ε

, és ugyanúgy

D^{*}

-ból

90^{\circ} - δ

vagy

90^{\circ} + δ

, ezek

2 - 2

körívet adnak mértani helyül a választott félsíkon:

D^{*}

számára az

i_{1}

i_{2}

párat,

E^{*}

számára

j_{1}

j_{2}

párat.
És mivel még

D^{*} E^{*}

a háromszögnek

A^{*} B^{*}

-gal párhuzamos középvonala, tehát

\vec{D^{*} E^{*}} = {\vec{B^{*} A}}^{*} / 2

, azért

E^{*}

-nak az

i_{1}

i_{2}

-ből

{\vec{A^{*} B}}^{*} / 2

-vel való eltolásával előálló

i'_{1}

i'_{2}

ívpáron is rajta kell lennie, így

E^{*}

szóba jövő helyzetei az

i'_{1}

i'_{2}

ívpár közös pontjai

j_{1}

j_{2}

-vel. Tovább az I. megoldás szerint haladhatunk.

A feladat kitűzőjének megoldásvázlata alapján