| Feladat: | 1305. matematika gyakorlat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Gál Péter , Móri Tamás | ||
| Füzet: | 1971/május, 206 - 208. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Középpontos tükrözés, Gúlák, Térfogat, Tetraéderek, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1970/március: 1305. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Először azt mutatjuk meg, hogy bármely valódi háromoldalú gúlához ‐ vagyis ha , , , különböző pontok, nincsenek egy síkban (nincs közülük három egy egyenesen) ‐, megadható olyan valódi háromoldalú gúla ‐ más néven négylapú test, tetraéder ‐, melynek élét a , , és , , pontok felezik. 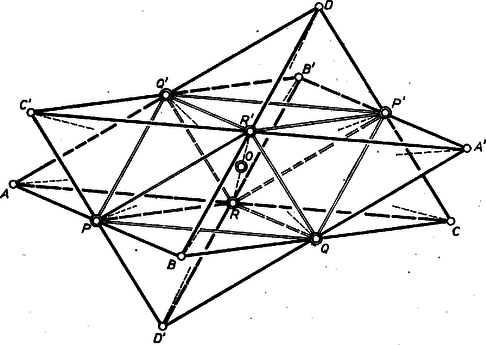 Mindezek szerint , , felezi rendre a , , szakaszt. És mivel nincs benne az síkban, hiszen tőle -szer akkora távolságban van, mint pl. , ez viszont ismét -szer annyira, mint , ami pedig a föltevés szerint nincs benne az síkban, azért a kapott egy a feladat követelményeinek megfelelő, valódi tetraéder. Úgy is mondhatjuk a távolságarányokat, hogy -nek -ből húzott, az lap síkjára merőleges magassága -szer akkora, mint -nak -ból induló magassága. S mivel a -vel szemben fekvő alapháromszög területe is -szer akkora, mint az -val szemben fekvő háromszögé, hiszen az háromszöget , és egybevágó háromszögre bontják, azért térfogata -szor akkora, mint térfogata. Máshogyan nem határozhatjuk meg a fenti laphoz a keresett tetraéder csúcsát, mert az sík nem alkalmas az lap céljára, hiszen csak -t tartalmaz az előírt élfelező pontok közül. Ugyanerre a -re jutunk akkor is, ha fenti eljárásunkat ismételve a háromszög helyett a , vagy , vagy az háromszögből indulunk ki, hiszen e háromszög a -ben ekvivalens szerepet játszik, mindegyik a egyik lapháromszögének a középháromszöge. Akkor viszont más tetraédert kapunk, ha a kiindulási háromszögünk csúcsai a "vesszős'' pont , vagy az egyik tükrös pontpárból a vesszős, a további két párból a vesszőtlen pont, pl. , , . Mivel azonban az új gúla mindegyik esetben -nek -ra való tükörképe, hiszen a most mondott háromszög mindegyike a föntebbi háromszög valamelyikének -ra való tükörképe, azért térfogata is -szorosa térfogatának. és -n túl nincs további megfelelő tetraéder, mert , , , , és közül már csak úgy lehetne pontot választani, hogy közülük kettő egymás képe legyen -ra, ilyen -asból pedig eljárásunkkal nem adódik tetraéder, hiszen pl. a , , pontok síkjában , és így is benne van. ‐ Ezzel vizsgálatunkat befejeztük.
Megjegyzés. A fenti 2 dolgozathoz fűzött megjegyzések említik a két gúla létezését és szimmetrikus voltát, másrészt tovább ezt olvassuk: "Nem mutattuk ki az tetraéder létezését , de ezt a feladat nem is írja elő.'' Az idézettel szemben a szerkesztőség a pontversenykiírást idézi: "mindig gondolják meg a versenyzők, létezik-e, lehetséges-e az mindig ‐ ill. mely feltételek mellett ‐, amiről beszélnek.'' A meggondolást kétes esetekben természetesen le is kell írni, ha a feladat nem is kérdezi. Pórázon vezetné a szerkesztőség a versenyzőket, ha maga mondana ki előre minden a megoldás során esetleg föllépő részletkérdést ‐ itt éppen a létezés vagy nem létezés, az egyértelműség fontos, gyakran fellépő kérdéseit ‐, amin a versenyző bemutathatná éleslátását, körültekintését. Megjegyezzük másrészt, hogy pl. egy gép részére szerkesztett számítási programban el kell várni a programozótól, hogy minden eshetőségre adjon utasítást a gépek. A mostani feladatunkhoz hasonló bizonyítást azonban egyelőre nem végeznek a gépek. Egy másik dolgozat ‐ némi helyes meglátással, de a sajnálatosan gyakori elnagyolással ‐ így ír: "Hasonló módszerrel még több ilyen tetraédert szerkeszthetünk.'' Ez viszont ‐ mint láttuk ‐ már sok, csak kettő van. |