Kezdőlap


Feladat:	1304. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Füzet:	1970/november, 140 - 142. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Síkidomok átdarabolása, Tengelyes tükrözés, Terület, felszín, Rombuszok, Szögfüggvények, síkgeometriai számítások, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1970/március: 1304. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Előkészítő megjegyzés az összes alábbi megoldásokhoz. Rajzoljuk meg az adott szabályos ötszög átlóit, ezek rendre párhuzamosak az ötszög egy-egy megfelelő oldalával, és egy újabb (konvex) szabályos ötszöget fognak közre, $A_{1} B_{1} C_{1} D_{1} E_{1}$ -et (a betűzést úgy választjuk, hogy az $A A_{1}$ , $B B_{1}$ stb. egyenesek e két ötszög közös szimmetriatengelyei legyenek). A $G F D$ háromszög egybevágó az $A B D_{1}$ háromszöggel, hiszen e két egyenlő szárú háromszög alapjai párhuzamosak és egyenlők, megfelelő száraik pedig párhuzamosak. Ugyancsak egybevágók az $A E G$ és $D E_{1} D_{1}$ háromszögek, hiszen megfelelő oldalaik párhuzamosak, és mivel $A D_{1} D G$ paralelogramma, azért $A G = D D_{1}$ . Alábbi megoldásainkban azt fogjuk belátni, hogy az $A B D_{1}$ és $D E_{1} D_{1}$ háromszögek területe egyenlő.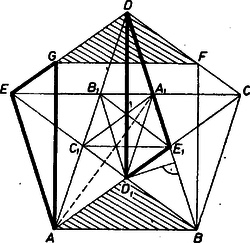

I. megoldás. Az

A B A_{1} E

négyszög rombusz, hiszen szemközti oldalai párhuzamosak és

A B = A E

. Emiatt

A

-t

B E

-re tükrözve

A_{1}

et kapjuk, és

A B D_{1}

, egybevágó

A_{1} B D_{1}

-gyel. Ez utóbbinak és a

D E_{1} D_{1}

háromszögnek közös része az

A_{1} D_{1} E_{1}

háromszög, az utóbbiból visszamaradó

A_{1} D D_{1}

háromszög egyenlő területű az

A_{1} B_{1} D

háromszöggel. Valóban, ahogy

A

-t

B E

-re tükrözve

A_{1}

-et kapjuk, ugyanúgy

D

-t a

C E

-re való tükrözés

D_{1}

-be viszi, tehát

A_{1} D B_{1} D_{1}

rombusz, melyet az

A_{1} B_{1}

D D_{1}

átlók négy egybevágó derékszögű háromszögre vágnak szét, a mondott

A_{1} D D_{1}

és

A_{1} B_{1} D

háromszög ezek közül kettő-kettő egyesítésével állítható elő. Az

A_{1} B_{1} D

háromszög pedig egybevágó az

A_{1} B D_{1}

háromszögből visszamaradó

B D_{1} E_{1}

háromszöggel, állításunkat tehát bebizonyítottuk.
Bizonyításunk során tulajdonképpen többet mutattunk meg, ti. azt, hogy a két háromszög egymásba átdarabolható: ha a

D E_{1} D_{1}

háromszöget az

A_{1} D_{1}

A_{1} B_{1}

egyenesekkel három részre vágjuk, a keletkező három részből összeállítható az

A_{1} B D_{1}

háromszög.

II. megoldás. Az

A_{1} B D_{1}

D E_{1} D_{1}

háromszögek

D_{1}

csúcsa és ezzel szemközti oldaluk egyenese közös, tehát a

D_{1}

csúcshoz tartozó magasságuk egyenlő. Egyenlő a

D_{1}

-gyel szemközti oldaluk is, hiszen e két szakaszt a

C C_{1}

, tengelyre való tükrözés egymásba viszi át, ‐ e két háromszög területe tehát egyenlő.

Megjegyzés. Lényegében ugyanezt használja fel a következő megoldás. A

D E_{1} D_{1}

háromszög területe nem változik meg, ha

D_{1}

csúcsát a

D E_{1}

alappal párhuzamosan

B_{1}

-be toljuk. A kapott

D E_{1} B_{1}

háromszög egybevágó a

B A_{1} D_{1}

háromszöggel, hiszen e háromszögek a

C C_{1}

tengelyre tükrözve egymásba mennek át.

III. megoldás. A

B D_{1} E_{1}

B D_{1} C

háromszögek hasonlók, hiszen egyenlő szárúak, és az alapjukon fekvő egyik szögük közös. (

B C = D_{1} C

, mert mindkettő egyenlő

B_{1} C

-vel.) Emiatt

\begin{matrix} \frac{B D_{1}}{D_{1} E_{1}} = \frac{C B}{B D_{1}} = λ . \end{matrix}

(1)

D E_{1} D_{1}

háromszöghöz hozzávéve a nála ugyancsak

λ

-szor nagyobb területű

D D_{1} A

háromszöget (ugyanis e háromszögek területének hányadosa megegyezik a közös

D

csúcsukkal szemben fekvő alapjuk

\begin{matrix} \frac{A D_{1}}{D_{1} E_{1}} = \frac{B D_{1}}{D_{1} E_{1}} = λ \end{matrix}

hányadosával), az egyenlő szárú

A E_{1} D

háromszöget kapjuk. Az

A B D_{1}

háromszöghöz hozzávéve a nála

λ

-szor nagyobb területű

D_{1} B C

háromszöget (mert e háromszögek területének hányadosa megegyezik alapjuk

\begin{matrix} \frac{C D_{1}}{A D_{1}} = \frac{C B}{B D_{1}} = λ \end{matrix}

hányadosával), az egyenlő szárú

A B C

háromszöget kapjuk.

A B C

és

A E_{1} D

egybevágók, mert alapjaik egyenlők:

A C = A D

, és egyenlők az alapon levő szögeik is:

B C A ∢ = C A D ∢

. A

D E_{1} D_{1}

A B D_{1}

háromszögek területeinek

(1 + λ)

-szorosa tehát egyenlő, így területeik is egyenlők.

IV. megoldás. A

D E_{1} D_{1}

háromszög

D D_{1}

oldalához tartozó magassága a

C_{1} E_{1}

szakasz fele, és

C_{1} E_{1} = A_{1} D_{1} = B D_{1}

. Megmutatjuk, hogy a

D D_{1}

oldal kétszer akkora, mint az

A B D_{1}

háromszög

B D_{1}

oldalához tartozó magassága, ezzel belátjuk, hogy

D E_{1} D_{1}

és

A B D_{1}

területe egyenlő. Valóban,

A B D_{1}

egybevágó

A_{1} C D

-vel és ennek

A_{1} D

oldalához tartozó magassága fele

D D_{1}

-nek.

V. megoldás. A

D D_{1} E_{1}

háromszög területe

\begin{matrix} \frac{1}{2} D E_{1} \cdot E_{1} D_{1} sin 108^{\circ}, \end{matrix}

hiszen e háromszög

E_{1}

-nél levő szöge egyenlő a szabályos ötszög csúcsainál levő szöggel.

A B D_{1}

területe pedig

\begin{matrix} \frac{1}{2} A D_{1} \cdot D_{1} B sin 108^{\circ}, \end{matrix}

E két kifejezés egyenlősége következik (1)-ből, hiszen

\begin{matrix} A D_{1} = D_{1} B és B C = D E_{1} . \end{matrix}