Kezdőlap


Feladat:	1299. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Angyal József
Füzet:	1971/március, 116 - 117. oldal		PDF \| MathML
Témakör(ök):	Diszkusszió, Körérintési szerkesztések, Gyakorlat
Hivatkozás(ok):	Feladatok: 1970/február: 1299. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A négy egyenest az $e_{1}$ , $e_{2}$ , $f_{1}$ , $f_{2}$ betűzéssel ellátva tekintjük adottnak, és olyan $k_{i}$ kört keresünk $(i = 1, 2)$ , mely érinti $e_{i}$ -t és $f_{i}$ -t, továbbá $k_{i}$ -nek $e_{i}$ -vel, $f_{i}$ -vel párhuzamos másik érintője $k_{3 - i}$ -t (azaz a másik kört). Csak olyan helyzettel foglalkozunk, amelyben $e_{i}$ és $f_{i}$ nem párhuzamosak.
Bármely kör két egymással párhuzamos érintőjének távolsága egyenlő a kör átmérőjével. Így, ha $e$ a két körre nézve külső közös érintő volt ‐ más szóval, ha $k_{1}$ és $k_{2}$ az $e$ -nek ugyanazon a partján voltak, tehát ugyanez állt $e_{1}$ -re és $e_{2}$ -re is ‐, akkor $e_{1}$ és $e_{2}$ távolsága megadja a körök (valamilyen sorrendben) $2 R$ és $2 r$ átmérőinek $(2 R ≧ 2 r)$ különbségét. Ha viszont $e$ belső közös érintő volt, vagyis szétválasztotta $k_{1}$ -et és $k_{2}$ -t, tehát ugyanígy $e_{1}$ -et és $e_{2}$ -t is, akkor $e_{1}$ és $e_{2}$ távolsága az átmérők összegét adja meg. Ugyanezek érvényesek természetesen a $f_{1}$ és $f_{2}$ közti távolságra.

I. Ha mármost az

e_{1}

és

e_{2}

közti

d_{e}

és az

f_{1}

és

f_{2}

közti

d_{f}

távolság egymástól különböző, akkor nagyobbikuk

2 (R + r)

-rel, kisebbikük pedig

2 (R - r)

-rel egyenlő. Föltehetjük, hogy

d_{e} > d_{f}

‐ hiszen ezt, ha kell, az

e

f

betűk fölcserélésével elérhetjük ‐, így

R

d_{e} + d_{f}

távolságösszeg negyede,

r

pedig a

d_{e} - d_{f}

különbség negyede. (Ha

f_{1}

és

f_{2}

egybeesnek, ez azt jelenti, hogy

R = r

.) Azt is kapjuk ebből, hogy az egymástól nagyobb távolságban haladó

e_{1}

és

e_{2}

a két kör egyik közös belső

e

érintőjével párhuzamosak, amely tehát köztük haladt, egyiküktől

2 R

, másikuktól

2 r

távolságban, és így

k_{1}

és

k_{2}

középpontja egyaránt

e_{1}

és

e_{2}

között volt; a kisebb távolságú

f_{1}

és

f_{2}

pedig a körök egyik közös

f

külső érintőjével párhuzamosak, ez a közös érintő az

f_{1}

és

f_{2}

közti síksávon kívül haladt, a hozzá közelebbi

f_{i}

-től

2 r

távolságban.
Ezek alapján

k_{1}

-nek

O_{1}

középpontja rajta van egyrészt az

e

és

e_{1}

közti, másrészt az

f

és

f_{1}

közti síksáv szimmetriatengelyén, vagyis

O_{1}

e két tengely metszéspontja;

k_{2}

-nek

O_{2}

középpontja pedig az

e

és

e_{2}

, valamint

f

és

f_{2}

közti síksávok szimmetriatengelyének metszéspontja, és ezzel maguk a körök is meg vannak határozva.
Az előbbiek alapján

e

-ként és

f

-ként egyaránt 2 ‐ 2 egyenes jön szóba aszerint, hogy

k_{1}

és

k_{2}

közül

k_{1}

sugarát tekintjük kisebbnek, ill. nagyobbnak, de e 2 ‐ 2 egyenes

e_{1}

és

f_{1}

indexelése alapján

2

párba kapcsolható. Így a feltételeket két

k_{1}

k_{2}

körpár teljesíti, a megfelelő középpontok az 1. ábrán

e

és

f

-hez

O_{1}

és

O_{2}

‐ ekkor

k_{1}

sugara kisebb ‐, továbbá

e^{*}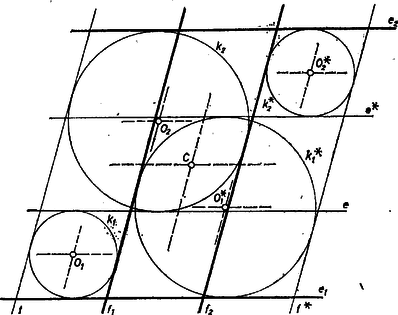

és

f^{*}

-hoz

O_{1}^{*}

és

O_{2}^{*}

A két megoldás egymás tükrös párja az

e_{1}

és

e_{2}

közti, valamint a

f_{1}

és

f_{2}

közti síksávok szimmetriatengelyeinek

C

metszéspontjára nézve.
Ezek szerint

d_{e} > d_{f}

esetén csak akkor mondhatjuk, hogy az

e_{1}

e_{2}

f_{1}

f_{2}

egyenesekből visszaállítottuk a kiindulási köröket, ha még azt is felhasználhatjuk, hogy

k_{1}

és

k_{2}

közül melyiknek a sugara volt nagyobb. A "visszaállítás'' szót kissé lazábban értelmezve viszont ezt mondhatjuk: a két kör vagy

k_{1}

és

k_{2}

volt, vagy

k_{1}^{*}

és

k_{2}^{*}

, így a visszaállítás kétértelmű.

II. Amennyiben viszont a

d_{e}

és

d_{f}

távolságok egyenlők ‐ más szóval

e_{1}

e_{2}

f_{1}

f_{2}

egy rombusz oldalegyenesei ‐, úgy vagy

2 (R - r)

-re, vagy

2 (R + r)

-re két (egyező) adatunk van, a másikukra pedig nincs adatunk, ezért

R

r

és a körök nem határozhatók meg. Bármely

r

-et választva, található hozzá megfelelő

R

, így a kiindulási helyzet visszaállításáról még tágabb értelemben sem lehet szó.

Angyal József (Budapest, Berzsenyi D. Gimn., III. o. t. )