Kezdőlap


Feladat:	1293. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Kovalcsik András , Turán Gyürgy
Füzet:	1970/november, 135 - 137. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Terület, felszín, Síkgeometriai számítások trigonometria nélkül négyszögekben, Síkgeometriai számítások trigonometria nélkül sokszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1970/január: 1293. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Legyen a két téglalap $T$ és $T_{1}$ , közös középpontjuk $O$ , oldalaik hossza $a$ és $b$ , ahol $a \geq b$ . $T_{1}$ mindegyik oldala $45^{\circ}$ szöggel hajlik $T$ mindegyik oldalához, így a két idom $a$ hosszúságú $C D$ és $C_{1} D_{1}$ oldalfelezői (hossztengelyei) is $45^{\circ}$ szöget zárnak be ( $C O C_{1} ∢ = 45^{\circ}$ , $C_{1} O D ∢ = 135^{\circ}$ ), és a $T$ -ből és $T_{1}$ -ből álló $X$ alakzat szimmetrikus az ezek közti szögek $t_{1}$ , $t_{2}$ felezőire, mint tengelyekre nézve.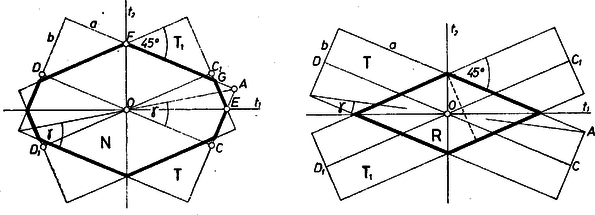

Ezeken tükrözve

T

és

T_{1}

egymásba mennek át,

C D

C_{1} D_{1}

-be, ill.

D_{1} C_{1}

-be. Legyen még

T

-nek a

C O C_{1}

, szögtartományban (

a = b

esetén az

O C_{1}

száron) levő csúcsa

A

. Így

T

és

T_{1}

, közös része egy

N

nyolcszög vagy egy

R

rombusz aszerint, hogy

C A

nagyobb

C_{1} A

-nál vagy nem (egyenlőségük esetén

A

a rombusz egyik csúcsa); mondhatjuk így is: a közös rész nyolcszög, ha

A O C ∢ > 45^{\circ} / 2 =

= 22, 5^{\circ}

, különben rombusz. Az

X

által (egyszeresen) lefedett terület pedig

2 a b - N

, ill.

2 a b - R

, ahol

N

R

az illető idom területét is jelöli.
II. Az első esetben

T

-nek

A

-ból induló,

b

hosszúságú oldala

t_{1}

-en metszi

T_{1}

nek

b

hosszúságú oldalát az

E

pontban, az

a

hosszúságú oldalát pedig

t_{2}

-n az

F

pontban és még egyszer

G

-ben. Ekkor

X

-et úgy kapjuk, hogy

T

-hez hozzáveszünk két-két

G E

, ill.

G F

átfogójú, egyenlő szárú, derékszögű háromszöget (hiszen

N

egyenlő

T

és a

4

háromszög területének különbségével).
A két átfogó hossza kiszámítható a következő egyenletrendszerből:

\begin{matrix} \frac{1}{\sqrt[]{2}} \cdot G E + (1 + \frac{1}{\sqrt[]{2}}) G F = a, \\ (\frac{1}{\sqrt[]{2}} + 1) G E + \frac{1}{\sqrt[]{2}} \cdot G F = b \end{matrix}

(

a

és

b

mindegyike tartalmazza a kétféle háromszög egy-egy befogóját, továbbá egyet-egyet az átfogók közül), éspedig

\begin{matrix} G E = \frac{1}{\sqrt[]{2}} (b - (\sqrt[]{2} - 1) a), G F = \frac{1}{\sqrt[]{2}} (a - (\sqrt[]{2} - 1) b), \end{matrix}

ahonnan a

4

háromszög területének összege

\begin{matrix} 2 (\frac{G E^{2}}{4} + \frac{G F^{2}}{4}) = (1 - \frac{1}{\sqrt[]{2}}) (a^{2} + b^{2} - \sqrt[]{2} a b), \end{matrix}

és ezt

a b

-vel növelve az

X

alakzat területe

\begin{matrix} X_{1} = (1 - \frac{1}{\sqrt[]{2}}) {(a + b)}^{2} . \end{matrix}

Eredményünk addig érvényes, amíg

G E \geq 0

, azaz

b / a \geq \sqrt[]{2} - 1

(és persze

b / a \leq 1

). Ez a korlát éppen

tg (45^{\circ} / 2)

, vagyis azt kívánja, hogy a

T

átlója és hossztengelye közti

γ

szög ne legyen kisebb

22, 5^{\circ}

-nál, amit az ábra szemléletéből is kiolvastunk. (

G F

viszont mindig pozitív.
A második esetben

R

oldala egyenlő a

b

befogójú, egyenlő szárú, derékszögű háromszög átfogójával, magassága pedig maga

b

, így az alakzat területe

\begin{matrix} X_{2} = 2 a b - \sqrt[]{2} b^{2}, \end{matrix}

hacsak

\begin{matrix} \frac{b}{a} \leq \sqrt[]{2} - 1 = tg 22, 5^{\circ}, azaz ha A O C ∢ \leq 22, 5^{\circ} . \end{matrix}

III. Vizsgáljuk

X

és

T

területének

q

arányát, mint az oldalak

b / a = r

arányának függvényét, míg

r

1

-től

\sqrt[]{2} - 1

-ig; majd tovább

0

-ig csökken (azonban

r > 0

), más szóval

T

és

T_{1}

szélességét egyre csökkentve, hosszúságukat állandóan tartva.
Az első intervallumban

\begin{matrix} q = \frac{X_{1}}{a b} = (1 - \frac{1}{\sqrt[]{2}}) (\frac{b}{a} + 2 + \frac{a}{b}) = (1 - \frac{1}{\sqrt[]{2}}) (r + \frac{1}{r} + 2), \end{matrix}

(1)

és itt

r

csökkentésével a második tényező változó része monoton nő. Ha ugyanis

\sqrt[]{2} - 1 \leq r_{2} < r_{1} \leq 1

, akkor

\begin{matrix} (r_{2} + \frac{1}{r_{2}}) - (r_{1} + \frac{1}{r_{1}}) = (r_{1} - r_{2}) (\frac{1}{r_{1} r_{2}} - 1) > 0, \end{matrix}

mert mindkét tényezője pozitív. Így első kérdésünk szempontjából csak az

r = \sqrt[]{2} - 1

értékhez tartozó

q = \sqrt[]{2}

értékre van szükségünk. A második kérdés céljára az

r = 1

-hez tartozó (lehető legkisebb) érték:

q = 4 - 2 \sqrt[]{2} (= 1,172)

.
A

0 < r \leq \sqrt[]{2} - 1

intervallumban pedig

\begin{matrix} q = \frac{X_{2}}{a b} = 2 - \sqrt[]{2} r, \end{matrix}

(2)

r

csökkenésével ez is monoton nő,

r = \sqrt[]{2} - 1

esetén

q = \sqrt[]{2}

; másrészt minden

r

-re

q < 2

. Azaz

q

-nak nincs legnagyobb értéke, de bármilyen kicsi pozitív szám

ε

, van olyan

b / a

arány, amelyre

q > 2 - ε

(természetesen

ε < 2 - \sqrt[]{2}

).
IV. Az eddigiek szerint

q

értéke ‐ hacsak

q \geq 4 - 2 \sqrt[]{2}

‐ egyértelműen meghatározza

T

oldalainak

r

arányát, éspedig

\begin{matrix} 4 - 2 \sqrt[]{2} \leq q < \sqrt[]{2} \end{matrix}

esetén az (1)-ből adódó

\begin{matrix} r + \frac{1}{r} + 2 - (2 + \sqrt[]{2}) q = 0 \end{matrix}

másodfokú egyenlet

\sqrt[]{2} - 1

és

1

közti gyöke lesz az arány (tudjuk, hogy van ilyen gyök és csak egy, mert a másik gyök ennek reciproka, tehát

> 1

), továbbá

\begin{matrix} \sqrt[]{2} \leq q < 2 \end{matrix}

esetén pedig (2)-ből

\begin{matrix} r = \frac{2 - q}{\sqrt[]{2}} . \end{matrix}

Turán György (Budapest, Fazekas M. Gyak. Gimn., II. o. t.)

Kovalcsik András (Balassagyarmat, Balassi B. Gimn., II. o. t.)