Kezdőlap


Feladat:	1292. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1970/december, 208 - 209. oldal		PDF \| MathML
Témakör(ök):	Beírt kör, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Síkgeometriai számítások trigonometria nélkül háromszögekben, Alakzatba írt kör, Ellenpélda, mint megoldási módszer a matematikában, Gyakorlat
Hivatkozás(ok):	Feladatok: 1970/január: 1292. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Nevezzük $T$ tulajdonságúnak a háromszöget, ha beírt körének középpontja egyenlő távolságra van (legalább) két oldalfelező ponttól. Minden egyenlő szárú háromszög nyilvánvalóan $T$ tulajdonságú, a kérdéses oldalak szerepére a szárakat véve.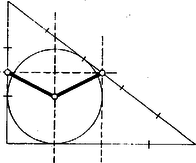
Másrészt könnyű adni különböző oldalú, $T$ tulajdonságú háromszöget is: ilyen a jól ismert, ún. ,,egyiptomi'' derékszögű háromszög, melynek két befogója $3$ és $4$ , átfogója $5$ egységnyi (1. ábra).

1. ábra

Ugyanis beírt körének sugara az ismert képlet szerint

ϱ = t / s = 1

egység,

1 / 4

része a hosszabbik befogónak, ezért középpontja rajta van a

3

egységnyi befogó és a vele párhuzamos középvonal közti sáv szimmetriatengelyén, a

3

és

5

egységnyi oldalak felezőpontjai pedig egymás tükörképei e tengelyre nézve, mert összekötő egyenesük párhuzamos a

4

egységnyi befogóval, tehát merőleges a tengelyre; így ez a két felezőpont egyenlő távolságra van a kör középpontjától.
Már ez az egyetlen ellenpélda elég ennek kimondásához: a feladatban megadott tulajdonságból nem következik, hogy a háromszögben van két egyenlő oldal. Ezzel a feladat kérdésére megadtuk a választ.

II. megoldás. Ha egy háromszög eleget tesz a feladatban leírt követelménynek, válasszuk úgy a betűzését, hogy beírt körének

O

középpontjától az

A

és

B

csúccsal szemben fekvő oldal

A_{1}

, ill.

B_{1}

felezőpontja legyen egyenlő távolságra, legyen továbbá a kör érintési pontja az oldalon

A_{0}

, ill.

B_{0}

. Az

O A_{1} A_{0}

és

O B_{1} B_{0}

derékszögű háromszögek

O A_{1} = O B_{1}

és

O A_{0} = O B_{0}

alapján egybevágók, és így (2‐4. ábrák):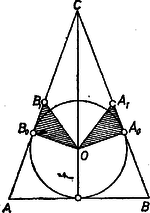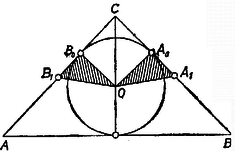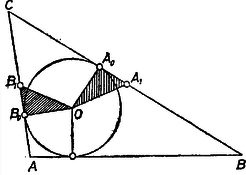

\begin{matrix} B_{0} B_{1} = A_{0} A_{1} . \end{matrix}

2. ábra

3. ábra

4. ábra

E két szakasz kifejezhető az

A_{0} C = B_{0} C

szakasszal, közös hosszuk, mint ismeretes,

s - c

C A_{1} = a / 2

-vel és

C B_{1} = b / 2

-vel, ha tudjuk, hogy

A_{0}

és

A_{1}

, valamint

B_{0}

és

B_{1}

közül melyik van közelebb

C

-hez:

\begin{matrix} A_{0} A_{1} = {\begin{matrix} C A_{1} - C A_{0} = \frac{a}{2} - (s - c), & ha C A_{1} \geq C A_{0}, \\ C A_{0} - C A_{1} = (s - c) - \frac{a}{2}, & ha C A_{1} < C A_{0}; \end{matrix} \end{matrix}

\begin{matrix} B_{0} B_{1} = {\begin{matrix} \frac{b}{2} - (s - c), & ha C B_{1} \geq C B_{0}, \\ (s - c) - \frac{b}{2}, & ha C B_{1} < C B_{0} . \end{matrix} \end{matrix}

A 2‐2 lehetőség

2 \cdot 2 = 4

-féleképpen állítható párba. Mindkétszer az alsót, vagy mindkétszer a felsőt véve:

\begin{matrix} \frac{a}{2} - (s - c) = \frac{b}{2} - (s - c), \end{matrix}

amiből

a = b

, a háromszög egyenlő szárú (magas, ill. lapos, 2‐3. ábrák); ha pedig

A_{0} A_{1}

-re a felső,

B_{0} B_{1}

-re az alsó lehetőséget vesszük (amiből

a > b

, hiszen

2 (s - c)

köztük levő érték):

\begin{matrix} \frac{a}{2} - (s - c) = (s - c) - \frac{b}{2}, akkor c = \frac{a + b}{2} \end{matrix}

(1)

(a hátra levő 4. párba állítás ugyanerre vezet, de

a < b

adódik, az egyenrangú szerepet játszó betűk fölcserélődnek, ez tehát nem lényegesen különböző eset), azaz a feltevésbeli

O A_{1} = O B_{1}

-ben nem szereplő oldal a másik kettőnek számtani közepe (és

a > c > b

).
Fenti meggondolásunk megfordításával könnyen belátható, hogy (1)-ből is következik, hogy

C A_{1} = C B_{1}

. Abból tehát, hogy a beírt kör középpontja egyenlő távolságra van két oldal felezőpontjától, nem következik, hogy a háromszög egyenlő szárú, csak annyit mondhatunk, hogy ebben az esetben a háromszög vagy egyenlő szárú, vagy az egyik oldal a másik kettő számtani közepe. (Szabályos háromszögeknél e kettő persze egyszerre teljesül.)