Feladat: 1286. matematika gyakorlat Korcsoport: 14-15 Nehézségi fok: nehéz
Megoldó(k):  Fejes Gábor ,  Pataki Béla ,  Smohay Ferenc 
Füzet: 1970/október, 67 - 68. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai szerkesztések, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):Feladatok: 1969/december: 1286. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. A jelölt a beszélgetésben nem hibázott. Megmutatjuk, hogy első két vállalása teljesíthető, harmadik válasza pedig azért helyes, mert a 18∘-os szög 1∘-os részekre osztását nem is lehet elvégezni kizárólag körző és vonalzó használatával. Ezt is indokolni fogjuk. A jelölt felvétele tehát azon múlott, hogy tudta-e teljesíteni vállalásait, ill. amennyiben ezt kérdezték, tudta-e indokolni harmadik állítását.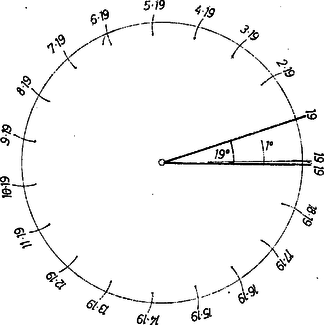
2. Az első két vállalás esetében elegendő egy 1∘-os szöget előállítani. Ez sokféleképpen lehetséges.
A 19∘ esetében ez elvégezhető úgy, hogy a szög csúcsa körül kört írunk és erre még 18-szor fölmérjük a 19∘-os szög szárai közti ívet, ekkor 192=360+1 miatt valóban 1∘-os szöget kapunk (1. ábra).

 
 
1. ábra
 

A 17∘-os szög esetében mérjük rá a csúcsa körül írt körre még 6-szor a szárai közti ívet, másrészt kétszer a kör sugarát. Ekkor a keletkező osztópontokhoz vezető egyenesek szöge 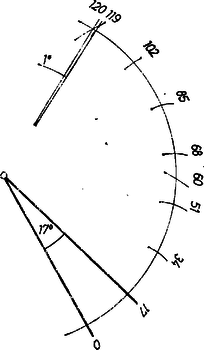120∘-7⋅17∘=1∘ (2. ábra).
 
 
2. ábra
 

3. A 18∘-os szög felosztása 1∘-os részekre egyértelmű lenne a szabályos 360-szög megszerkesztésével. Azonban Gauss megmutatta, hogy n=2kp1⋅p2⋅...⋅pm oldalú szabályos sokszög (ahol k nem negatív egész, a pi-k páratlan primek) akkor és csak akkor szerkeszthető körzővel, vonalzóval, ha a pi-k csupa különböző 2r+1 alakú prímek. Eszerint a 360=22⋅32⋅5 oldalú szabályos sokszög nem szerkeszthető, mert az oldalszám osztható a 3 páratlan prim négyzetével.
 

Fejes Gábor (Miskolc, Földes F. Gimn., II. o. t.)

Smohay Ferenc (Székesfehérvár, Teleki Blanka Gimn., II. o. t.)
 

Megjegyzések. 1. Vázolunk néhányat a megoldásokban talált további szerkesztési lehetőségek közül. Rövidítésül csak azt adjuk meg, hogy egy, a szögünk csúcsa köré írt körön mely középponti szög szárának metszéspontját jelöljük ki, a szög egyik szárától mérve.
Elég volna ismerni 2∘-ot is. Ezzel 0∘-ból indulva a páros sorszámú, 19∘-ból, ill. 17∘-ból visszafelé indulva a páratlan sorszámú osztásvonalakat kapjuk. Mármost kiadódik a 2∘ a könnyen szerkeszthető 30∘ és 2⋅19=38∘ közti 8∘-os szög kétszeri felezésével. Vagy ‐ mivel a felezés nehézkes ‐ haladhatunk a következő osztópontok kijelölésével is: 30∘, 38∘ (köztük 8∘), visszafelé 22∘, 14∘, 6∘, másrészt 0∘-ból előre a 8∘, így 8∘-6∘=2∘. Hasonlóan 2⋅17∘-30∘ fele 2∘.
Megtakaríthatjuk a 30∘ előállításához szükséges felezést így is: 0∘, 19∘, 38∘, 57∘, 60∘ (köztük 3∘); ezzel 3∘, 6∘,9∘, 12∘, 15∘, 18∘, végül a 19∘-18∘=1∘-os ívvel egy-egy körző-beszúrással 3∘-ból 2∘ és 4∘, 6∘-ból 5∘ és 7∘ stb.
Hasonlóan használható a 135∘(=3⋅45∘) és 15∘ vagy 75∘ is (ezekhez két-két felezés szükséges) és akkor 135∘-7⋅19∘=2∘, ill. 19∘-15∘=4∘, 4⋅19∘-75∘=1∘.
Számosan a még több szerkesztési lépéssel kiadódó 18∘-ot használták fel (18∘ a szabályos ötszög oldalához tartozó középponti szög negyede, ill. a szabályos 10-szögoldal középponti szögének fele).
Továbbiak: a 17∘-os szög esetében
0∘, 17∘; 60∘, 30∘, 15∘, innen a 17∘-ig 2∘.
0∘, 17∘ 34∘, 51∘; 60∘, 60∘-51∘ alapján 9∘ és vagy 17∘-9∘=8∘, vagy 2⋅9∘-17∘=1∘.
0∘, 17∘, 34∘, 51∘, 85∘; 90∘, az utóbbi 2-ből 5∘, majd 17∘-3⋅5∘=2∘.
2. Az első két és a 3. kérdés válasza közti látszólagos ellentmondás feloldása a következő: mind a 17∘-os, mind a 19∘-os szög megadása kiterjesztette az eukleidészi szerkesztéssel elvégezhető feladatok körét, mert eukleidészi módon egyik szög sem szerkeszthető meg; viszont a 18∘-os szög megadása nem segítség, mert olyasmit nyújt, amit magunk is meg tudnánk szerkeszteni a megengedett módon.
 

Pataki Béla (Budapest, I. István Gimn., II. o. t.)