Kezdőlap


Feladat:	1280. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Füzet:	1970/május, 203. oldal		PDF \| MathML
Témakör(ök):	Középvonal, Beírt kör, Hozzáírt körök, Trapézok, Érintőnégyszögek, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1969/november: 1280. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az eredeti háromszög $A B C$ , a középháromszöge $A_{1} B_{1} C_{1}$ és legyen a feltételt teljesítő oldal 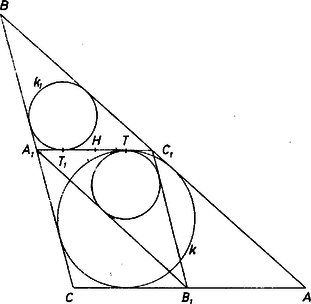$A C = (B A + B C) / 3$ .

Ekkor az

A C A_{1} C_{1}

trapéz érintőnégyszög, hiszen szemben fekvő oldalpárjainak összege egyenlő:

\begin{matrix} A C + A_{1} C_{1} = \frac{3}{2} A C = \frac{B A + B C}{2} = A C_{1} + C A_{1} . \end{matrix}

Eszerint pedig a trapézunkba beírt kör azonos az

A B C

háromszögbe írt

k

körrel, mert belülről érinti annak mindhárom oldalát, ilyen kör pedig csak egy van. Ennélfogva

k

érinti az

A_{1} C_{1}

középvonalszakaszt, legyen az érintési pont

T

.
Legyen még

k_{1}

A_{1} C_{1} B

háromszögbe írt kör, ez érintse

A_{1} C_{1}

-et a

T_{1}

pontban. Mivel

k_{1}

és

k

A_{1} B C_{1}

háromszög belső és külső érintő körei, az

A_{1} C_{1}

oldalon levő érintési pontjaik szimmetrikusan helyezkednek el az

A_{1} C_{1}

oldal

H

felezőpontjára nézve. (Ugyanis

C_{1} T = A_{1} T_{1}

, mert mindkettő egyenlő az

A_{1} B C_{1}

háromszög fél kerületének és

B C_{1}

oldalának a különbségével.)
A

k_{1}

kört

H

-ra tükrözve az

A_{1} B_{1} C_{1}

középháromszögbe írható kört kapjuk, ez az

A_{1} C_{1}

egyenest

T_{1}

-nek

H

-ra vonatkozó tükörképében,

T

-ben érinti, itt tehát érinti

k

-t is. Ezt kellett bizonyítanunk.