Kezdőlap


Feladat:	1279. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Arvay L. , Bacsó G. , Balog J. , Balogh Z. , Bodnár István , Breuer P. , Csernátony Géza , Domokos Mária (Makó) , Fazekas I. , Forró S. , Füredi Z. , Gál Péter , Gál Tibor , Győri E. , Hermann P. , Horváth Ferenc , Horváth Jenő , Horváth László , Horváth Mária , Kertész Á. , Kirchner I. , Kovács I. , Kramer A. , Langsádi I. , Lévai Miklós , Major Imre , Molnár Gy. , Molnár József , Móri T. , Oláh Vera , Pach J. , Pap Gy. , Reiczigel J. , Szarka Imre , Tarsó B. , Tegze M. , Turán Gy. , Varga György , Varga Mária
Füzet:	1970/szeptember, 22 - 24. oldal		PDF \| MathML
Témakör(ök):	Párhuzamos szelők tétele, Diszkusszió, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1969/november: 1279. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. Jelöljük az adott szakaszokat $m_{a}$ , $m_{b}$ -vel úgy, hogy $m_{a} \leq m_{b}$ legyen, így a háromszög harmadik magassága $m_{c} = m_{a} + m_{b}$ . A háromszög $t$ területét felhasználva a rájuk merőleges oldalak rendre:

\begin{matrix} a = 2 t \frac{1}{m_{a}}, b = 2 t \frac{1}{m_{b}}, c = 2 t \frac{1}{m_{c}} . \end{matrix}

Innen

\begin{matrix} a : b : c = \frac{1}{m_{a}} : \frac{1}{m_{b}} : \frac{1}{m_{c}}, \end{matrix}

(1)

vagyis a háromszög oldalainak arányát megadja a megfelelő magasságok reciprokainak aránya. Az utóbbiak ismeretében a keresetthez hasonló háromszöget szerkesztünk, majd ezt úgy nagyítjuk (ill. kicsinyítjük), hogy legkisebbik magassága

m_{a}

legyen.
2. Egy tetszés szerinti szakaszt hosszúságegységnek választva a magasságok reciproka szerkeszthető, pl. egy szög szárait párhuzamos egyenesekkel metszve. Legyen

m_{b} = 1

, mérjük fel ezt a szakaszt az

X_{0} O X'

szög

O X_{0}

szárára ‐ legyen a végpontja

B_{0}

‐ ,

O X'

-re pedig az

O A' = m_{a}

O B' = m_{b} (= 1)

és

O C' = m_{c} = m_{a} + m_{b}

szakaszt és húzzuk meg a párhuzamost

B'

-n át

A' B_{0}

-lal és

C' B_{0}

-lal, az

O X_{0}

-lal való

A_{0}

, ill.

C_{0}

metszéspontig (1. ábra).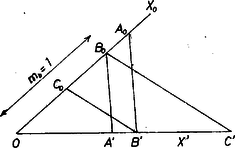

1. ábra

Ekkor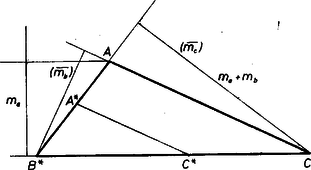

\begin{matrix} O A_{0} : O B_{0} = O B' : O A' és O C_{0} : O B_{0} = O B' : O C' \end{matrix}

alapján az

O A_{0} = 1 / O A' = 1 / m_{a} = a_{0}

O C_{0} = 1 / m_{c} = c_{0}

, továbbá

1 / m_{b} = O B_{0} = b_{0}

szakaszokból szerkesztett

A^{*} B^{*} C^{*}

háromszög hasonló a keresetthez. Ezért a

B^{*} A^{*}

egyenest

B^{*} C^{*}

-tól

m_{a}

távolságban, az

A

pontban metszve, végül a

B^{*} C^{*}

egyenest az

A

-n átmenő,

A^{*} C^{*}

-gal párhuzamos egyenessel

C

-ben metszve,

A B^{*} C

egy a követelményt kielégítő háromszög (2. ábra).

2. ábra

3. Valóban az

A B^{*} C

háromszög

A

-ból induló magassága

m_{a}

, és véve a

B^{*}

-ból és

C

-ből húzott

\bar{m_{b}}

, ill.

\bar{m_{c}}

magasságait, ezek reciprokainak aránya (1), valamint a végzett szerkesztések szerint:

\begin{matrix} \frac{1}{m_{a}} : \frac{1}{\bar{m_{b}}} : \frac{1}{\bar{m_{c}}} = B^{*} C : C A : A B^{*} = B^{*} C^{*} : C^{*} A^{*} : A^{*} B^{*} = O A_{0} : O B_{0} : O C_{0}, \end{matrix}

továbbá egyrészt

\begin{matrix} \frac{1}{m_{a}} : \frac{1}{\bar{m_{b}}} = O A_{0} : O B_{0} = O B' : O A' = 1 : m_{a}, \end{matrix}

innen

\bar{m_{b}} = 1 = m_{b}

; másrészt

\begin{matrix} \frac{1}{\bar{m_{b}}} : \frac{1}{\bar{m_{c}}} = O B_{0} : O C_{0} = O C' : O B' = (m_{a} + m_{b}) : 1, \end{matrix}

innen pedig a legutóbbi eredmény alapján

\begin{matrix} \bar{m_{c}} = m_{a} + m_{b} . \end{matrix}

4. A szerkesztés végrehajtható volta csak azon múlik, létrejön-e az

A^{*} B^{*} C^{*}

háromszög, vagyis legnagyobb oldala kisebb-e a másik kettő összegénél, azaz teljesül-e

\begin{matrix} \frac{1}{m_{a}} < \frac{1}{m_{b}} + \frac{1}{m_{a} + m_{b}} . \end{matrix}

Innen rendezéssel

\begin{matrix} {(\frac{m_{a}}{m_{b}})}^{2} + (\frac{m_{a}}{m_{b}}) > 1, {(\frac{m_{a}}{m_{b}} + \frac{1}{2})}^{2} > \frac{5}{4}, \end{matrix}

ugyanis a szakaszok pozitívok. Eszerint a szerkesztés végrehajtható, ha

\begin{matrix} (0, 618 \approx) \frac{\sqrt[]{5} - 1}{2} < \frac{m_{a}}{m_{b}} \leq 1. \end{matrix}

Bodnár István (Eger, Gárdonyi G. Gimn., II. o. t.)

Csernátony Géza (Budapest, L László Gimn., II. o. t.)

Lévai Miklós (Tata, Eötvös J. Gimn., I. o. t.)

Szarka Imre (Komárno, Ált. Középisk., Szlovákia)

Megjegyzés. Megemlítünk két más eljárást szakaszok reciprokának, ill. azzal arányos szakasznak szerkesztésére. A

D E = 1

szakaszra

E

-ben merőlegesen álló

e

egyenesre felmérjük az

E F = m

szakaszt, majd

e

-t metsszük az

F D

-re

D

-ben állított merőlegessel a

G

pontban, ekkor

E G = 1 / m

(3. 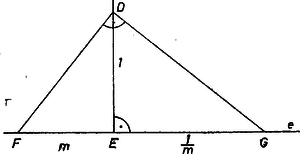ábra).

3. ábra

Egy

k

kör (egymáshoz elég közel választott)

P

és

Q

pontja körül kört írunk

m_{a}

, ill.

m_{b}

sugárral, majd ezeknek a körön kívül fekvő

R

metszéspontja körül

m_{a} + m_{b}

sugárral. Jelöljük

k

-nak az utóbbi körrel való egyik metszéspontját

S

-sel, továbbá az

R P

R Q

R S

egyenessel való második metszéspontját rendre

P_{1}

gyel,

Q_{1}

-gyel,

S_{1}

gyel (4. ábra).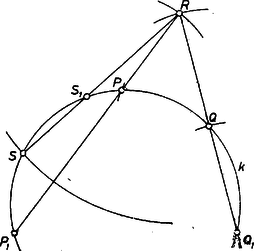

4. ábra

Ekkor

R P \cdot R P_{1} = R Q \cdot R Q_{1} = R S \cdot R S_{1} = állandó = p^{2}

(

p

R

-ből

k

-hoz húzott érintő hossza), és pl.

R P_{1} = p^{2} / m_{a}

. (V.L.)

II. megoldás. Tekintsünk el egyelőre az

m_{c} = m_{a} + m_{b}

összefüggéstől, és legyen

m_{c}

is független adat. Az (1)-ben látott fordított arányosságot felhasználó, tetszetős elgondolás a következő. Azt, hogy az oldalak arányosak a megfelelő magasságok reciprokával, úgy is mondhatjuk, hogy az oldalak reciprokai arányosak a megfelelő magasságokkal. Szerkesszünk tehát segédháromszöget

m_{a}

-ból,

m_{b}

-ből és

m_{c}

-ből mint oldalakból és tekintsük ennek (rendre)

μ_{a}

μ_{b}

μ_{c}

magasságát. Ezek is és a keresett háromszög oldalai is olyan (összetett) arányban vannak, mint

(1 / m_{a}) : (1 / m_{b}) : (1 / m_{c})

, tehát a

μ_{a}

-ból,

μ_{b}

-ből és

μ_{c}

-ből mint oldalakból szerkesztett háromszög hasonló a keresetthez. Ebből a már látott módon kaphatjuk a keresett háromszöget.
Az elgondolásnak azonban van egy szépséghibája; a háromszög magasságaiból nem mindig szerkeszthető háromszög. (Gondoljunk hegyes ék alakú egyenlő szárú háromszögre, ilyen már az

1

3

3

oldalakkal szerkesztett háromszög is.) Eredeti feladatunkban is ez a helyzet. Eljárhatunk azonban úgy, hogy a segédháromszöget (a mondott helyett) a

\begin{matrix} 2 m_{a}, m_{b}, m_{a} + m_{b} \end{matrix}

szakaszokból szerkesztjük mint oldalakból. Ebben a

μ_{a}^{*}

μ_{b}

μ_{c}

magasságok aránya

\begin{matrix} μ_{a}^{*} : μ_{b} : μ_{c} = \frac{1}{2 m_{a}} : \frac{1}{m_{b}} : \frac{1}{m_{a} + m_{b}} = \frac{a}{2} : b : c \end{matrix}

(ahol

a

b

c

a keresett háromszög oldalai), ezért a

2 μ_{a}^{*}

μ_{b}

μ_{c}

szakaszokból mint oldalakból szerkesztett háromszög hasonló a kívánthoz. ‐ Ezt tudva az I. megoldás záró része szerint járhatunk el.
A segédháromszög az alkalmazott fogással megszerkeszthető (mert legnagyobb oldala

m_{a} + m_{b}

), ez azonban nem biztosítja, hogy a

2 μ_{a}^{*}

μ_{b}

μ_{c}

szakaszokból mindig kapunk háromszöget. Ennek feltételéül ugyanazt kapjuk, mint az I. megoldásban.