Kezdőlap


Feladat:	1275. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Császár Gyula , Hetzmann Antal , Kovács István
Füzet:	1970/május, 200. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1969/október: 1275. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a háromszög átfogója $A B$ , és legyen rajta $P$ , $Q$ a $B C$ , ill. $A C$ befogóra az $E$ , ill. $F$ felező pontban állított merőlegesen.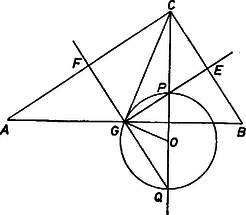

Így a

C P E

és a

Q C F

háromszög hasonló az

A B C

háromszöghöz, mert a csúcsok felsorolása szerint páronként megfelelő oldalaik merőlegesek egymásra, tehát az oldalpárok aránya egyenlő:

\begin{matrix} \frac{C P}{A B} = \frac{C E}{A C} = \frac{C B}{2 A C}, \frac{C Q}{B A} = \frac{C F}{B C} = \frac{C A}{2 B C}, \end{matrix}

innen

\begin{matrix} \sqrt[]{C P \cdot C Q} = \sqrt[]{\frac{A B \cdot C B}{2 A C} \cdot \frac{B A \cdot C A}{2 B C}} = \frac{A B}{2}, \end{matrix}

amit bizonyítanunk kellett.

Hetzmann Antal (Tatabánya, Árpád Gimn., I. o. t.)

Megjegyzés. Ha a befogók egyenlők, akkor

P

és

Q

egybeesik az átfogó

G

felezőpontjával, az állítás semmitmondó,

C P = C Q = C G = A B / 2

, hiszen ekkor

C G A

is egyenlő szárú derékszögű háromszög.

Császár Gyula (Budapest, Berzsenyi D. Gimn., I. o. t.)

II. megoldás. A fenti jelölésekkel elég azt belátnunk, hogy a

P Q

átmérőjű,

O

középpontú kört a

C G

egyenes

G

-ben érinti, hiszen

C P

és

C Q

e körnek

C

-ből húzott szelői, mert

P

is,

Q

is abban az

A C B

derékszögtartományban vannak, mint maga az

A B C

háromszög, másrészt

C G = G A = A B / 2

, hiszen

G

A B C

háromszög köré írt kör középpontja.

G

rajta van a

P Q

átmérőjű körön, mert itt metszi egymást a két felező merőleges, amelyek pedig egymásra is merőlegesek. Választhatjuk a betűzést úgy, hogy

C A > C B

legyen, ekkor

P

G E

szakaszon,

Q

pedig az

F G

meghosszabbításán adódik,

C P < C Q

, ezért az

O C G

háromszögben

\begin{matrix} P O G ∢ + G C O ∢ = 2 P Q G ∢ + G C O ∢ = (G A C ∢ + Q C B ∢) + O C G ∢ = \\ = G C A ∢ + G C B ∢ = A C B ∢ = 90^{\circ}, \end{matrix}

hiszen

G A C

egyenlő szárú háromszög. Eszerint

G C

merőleges a

G O

sugárra. Ezt akartuk bizonyítani.

Kovács István (Budapest, I. István Gimn., II. o. t.)