Kezdőlap


Feladat:	1269. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Füzet:	1970/február, 61 - 62. oldal		PDF \| MathML
Témakör(ök):	Nevezetes azonosságok, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1969/szeptember: 1269. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $A B = A C = b$ és $B D = a$ , így $D F = D G = D E = a \sqrt[]{2}$ , legyen továbbá $H$ az $A D$ egyenes $G$ -t tartalmazó partján, és $H$ vetülete a $B C$ egyenesen 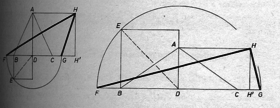$H'$ .

Így

F H > G H

, továbbá

F H' = D F + D H' = D F + A H = b + a \sqrt[]{2}

és

G H' = | D H - D G | = | b - a \sqrt[]{2} |

, ezért

\begin{matrix} F H = \sqrt[]{F H^{' 2} + H' H^{2}} = \sqrt[]{{(b + a \sqrt[]{2})}^{2} + D A^{2}} = \\ = \sqrt[]{(b^{2} + 2 \sqrt[]{2} a b + 2 a^{2}) + (b^{2} - a^{2})} = \sqrt[]{2 b^{2} + 2 \sqrt[]{2} a b + a^{2}} = b \sqrt[]{2} + a, \end{matrix}

hiszen szakasz hossza pozitív. Hasonlóan

\begin{matrix} G H = \sqrt[]{G H^{' 2} + H' H^{2}} = \sqrt[]{{(b - a \sqrt[]{2})}^{2} + (b^{2} - a^{2})} = b \sqrt[]{2} - a, \end{matrix}

ugyanis

b \sqrt[]{2} > b > a

Ezek alapján

F H - G H = 2 a = B C

Megjegyzés. Az

F H - G H

különbség fenti eredményünk szerint a háromszögnek csak az alapjától függ: ha az

A

pont helyzetét változtatjuk (míg

B

és

C

rögzített), az előírás szerint szerkesztett

H

pont minden helyzetében az

F H - G H

különbség értéke ugyanaz lesz. A

H

pont tehát egy hiperbolán fut végig, hiszen

F

és

G

is rögzítettek.
Ismerve a hiperbola koordináta-rendszerbeli egyenletét, ezt az eredményt (és ebből feladatunk állítását) rövidebben is megkaphattuk volna: válasszuk a

B C

D A

egyeneseket egy koordináta-rendszer tengelyének, akkor a

H

pont

H' D = x

és

H' H = y

koordinátái között

\begin{matrix} x^{2} = D H^{' 2} = A B^{2}, y^{2} = D A^{2} \end{matrix}

alapján az

\begin{matrix} x^{2} - y^{2} = B D^{2} \end{matrix}

összefüggés áll fenn. Ez egy hiperbola egyenlete, melynek fókuszai valóban a feladat szerinti

F

és

G

pontok.