Feladat: 1255. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Angyal J. ,  Balogh Z. ,  Boros E. ,  Czédli Gábor ,  Egyedi D. ,  Engedi D. ,  Farkas P. ,  Fodor Éva ,  Fodor Péter ,  Garay B. ,  Gáspár Gy. ,  Hadik Gy. ,  Horváth András ,  Juhász Judit ,  Kirchner Imre ,  Kiss Mária ,  Komornik V. ,  Nagy Csaba ,  Nagy Zsuzsa ,  Pap Gy. ,  Pataki Béla ,  Pataki L. ,  Pattantyús P. ,  Péter Erika ,  Petz D. ,  Pintér I. ,  Reviczky J. ,  Sashegyi L. ,  Sváb J. ,  Szabados Gy. ,  Zámolyi F. 
Füzet: 1969/december, 209 - 211. oldal  PDF  |  MathML 
Témakör(ök): Beírt alakzatok, Síkgeometriai számítások trigonometria nélkül sokszögekben, Szélsőérték-feladatok differenciálszámítás nélkül, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):Feladatok: 1969/április: 1255. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a kérdéses hatszög ABCDEF=H úgy, hogy AB=5,BC=6,...,FA=7+x. Tükrözzük a rögzített oldalakból álló ABCD törött vonalat az AD szakasz O felezőpontjára a DB'C'A helyzetbe, így B', C' a DE, ill. AF félegyenesen lesz és B'C'∥CB∥EF, vagyis a B'C'FE négyszög trapéz, hacsak x≠0, és szárainak hossza 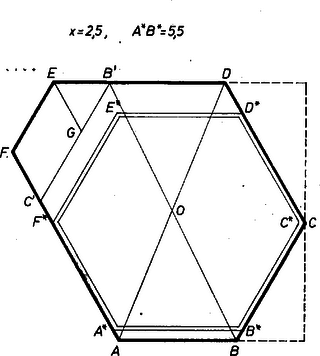|DE-DB'|=|AF-AC'|=|x|.

 

 

Húzzunk továbbá párhuzamost E-n át AF-fel, és messe ez a B'C' egyenest G-ben. Így C'FEG paralelogramma, B'G=|B'C'-EF|=|x|=C'F=GE=B'E, tehát EB'G egyenlő oldalú háromszög, hacsak x≠0. így oldalegyenesei páronként 60∘-os szögeket zárnak be, és ugyanez áll H oldalegyeneseire. Mivel pedig H konvex, csak a szomszédos oldalegyenesek közti külső szög lehet 60∘, tehát H mindegyik szöge 120∘, mint a szabályos hatszög szögei.
Ebből nyilvánvaló, hogy a H-ból egy darabban kivágott S szabályos hatszög úgy lesz a legnagyobb, ha oldalait a H oldalain, ill. ezekkel párhuzamosan helyezzük el, és S két szemben fekvő oldalának távolsága ‐ röviden: S szélessége ‐ legfeljebb annyi, mint a H párhuzamos oldalpárjai között adódó 3-féle távolság legkisebbike.
Mármost az AB és DE egyenesek távolsága annyi, mint a C csúcs tőlük mért távolságainak összege. Ezeket megadja a CB=6, ill. CD=7 oldalú szabályos háromszög magassága, így összegük 133/2. Hasonlóan AF és CD távolsága 113/2, kisebb az előbbinél, végül BC és EF távolsága (12+x)3/2, tehát S-nek d szélessége nem nagyobb, mint az utóbbi két távolság kisebbike.
Mármost
(12+x)32⋛1132,azaz12+x⋛11
aszerint, hogy
-1<x<6,x≠0;x=-1;-5<x<-1.Így  pedigSoldalhossza rendre︸112,ill.12+x2,


megmutatjuk ugyanis, hogy S-nek H-ba való alkalmas beillesztésével ez az oldalhossz el is érhető.
Az első esetben A*B*C*D*E*F*=S-nek 2-2 csúcsát illesztjük az AF, CD egyenespárra, éspedig C*-ot C-be. Így B* a CB oldalon lesz. BB*=1/2, és könnyen belátható, hogy A* az AF oldalon lesz, AA*=1/2, tehát A*F=(7+x)-1/2=x+13/2≧11/2, F* is AF-en lesz, x=-1 esetén éppen F-ben. Másrészt D* a CD oldalon van, és CD*=11/2<CD, így pedig az oldalak párhuzamossága és H konvexsége miatt E* is a H-ban v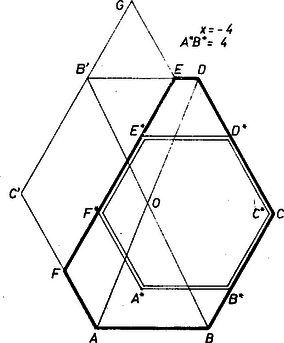an.
 

 

A második esetben a BC, EF egyenespárra helyezzük a B*C*, E*F* oldalakat, C*-ot ismét C-be. Így D*D=(2-x)/2, és B*B=-x/2 (ami >0), D*E* és B*A* a DE, BA párhuzamosok között halad, E*F*=(6-x)-EE*=(6-x)-DD*=(10-x)/2<(12+x)/2, tehát F* is E és F közé jut; úgy pedig A* is H-ban van.
x=0 esetén az EB'G háromszög ponttá zsugorodik, H szögeiről és S oldaláról semmit sem mondhatunk. Ekkor H centrálszimmetrikus, bármelyik két szemben fekvő oldala tetszés szerinti közel hozható egymáshoz.
Ezzel vizsgálatunkat befejeztük.
 

Czédli Gábor (Baja, III. Béla Gimn., II. o. t. )

Pataki Béla (Budapest, I. István Gimn., I. o. t. )