Kezdőlap


Feladat:	1250. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1970/március, 112 - 113. oldal		PDF \| MathML
Témakör(ök):	Hossz, kerület, Síkbeli ponthalmazok távolsága, Síkgeometriai számítások trigonometria nélkül háromszögekben, Síkgeometriai számítások trigonometria nélkül körökben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1969/március: 1250. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. $S$ -et először a kör rövidebb $P R$ ívén vesszük fel. Legyen egy az $A B O$ háromszögbe beírt háromszögnek az $A B$ oldalszakaszon levő csúcsa mindjárt $S$ , a $B O$ , $O A$ szakaszon $A'$ , ill. $B'$ (1. áb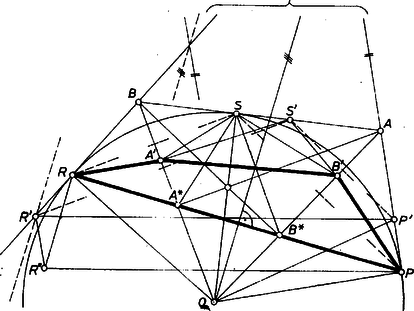ra).

1. ábra

E háromszög kerülete egyenlő a

P B' A' R

töröttvonal hosszával. Ugyanis

P

és

S

, mint az

A

-ból húzott érintők érintési pontjai, egymás tükörképei

O A

-ra mint tengelyre nézve, és ugyanígy

R

S

O B

tengelyre szimmetrikus pontpár, tehát

\begin{matrix} S B' + B' A' + A' S = P B' + B' A' + A' R . \end{matrix}

Ez valóban nem lehet kisebb a töröttvonal

P

R

végpontjai közti szakasznál, egyenlő is csak akkor vele, ha

A'

B'

szerepére azt az

A^{*}

B^{*}

pontját választjuk az

O B

, ill.

O A

szakasznak, amelyet a

P R

szakasz metsz ki belőle.

S

helyén az

A B

oldalszakasz más,

S'

pontját véve az

S' A' B'

háromszög kerülete az előzőkhöz hasonlóan egyenlő annak a

3

darabból álló törött vonalnak a hosszával, melynek kezdő és végpontja

S'

-nek az

O A

O B

tengelyre vett

P'

, ill.

R'

tükörképe, közbülső töréspontjai pedig

B'

és

A'

. Az ilyen törött vonalak hossza hasonlóan nem kisebb a

P' R'

szakasznál, így elég erről az utóbbiról belátnunk, hogy nem kisebb

P R

-nél.
Toljuk át

P' R'

-t a

P R''

helyzetbe. A keletkezett

P R R''

háromszögről mindjárt belátjuk, hogy

R

-nél derékszögű, ebből adódik, hogy

P R < P R'' = P' R'

. Valóban,

R' R'' = P' P = S' S = R' R

, így

R' R R''

egyenlő szárú háromszög,

R R''

párhuzamos az

R R'

és

R R''

irányok közti szög felezőjével, ez a szög pedig egyállású a

P

-ben,

R

-ben húzott érintők közti szöggel, aminek a felezője merőleges

P R

-re, tehát

R R'' ⊥ R P

.
Az

S

-re tett korlátozás alapján

P O R ∢ < 180^{\circ}

, így a felhasznált háromszögek valóban léteznek, és létezik a mondott

A^{*}

B^{*}

pont, hiszen a

P R

egyenes elválasztja

O

-t

P

-től. Ezzel az állítást bebizonyítottuk.

II. Ha

S

-et a nagyobbik

P R

köríven választjuk, fenti meggondolásunk érvényes marad, annyiban azonban módosul, hogy az

A O B

háromszögbe beírt

S A' B'

, ill.

S' A' B'

háromszögek között nem létezik a

P R

húr, ill. a

P' R'

szakasz hosszával egyenlő kerületű háromszög, hiszen az

O P

(ill.

O P'

) félegyenest

S

-en (ill.

S'

-n) át az

O R

(ill.

O R'

) félegyenesbe

180^{\circ}

-nál nagyobb elfordulás viszi át,

P R

-nek (ill.

P' R'

-nek) nincs pontja az

O A B

háromszög kerületén (2. ábra).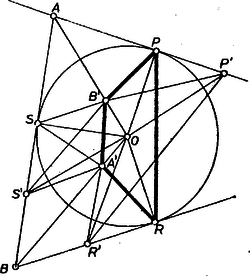

2. ábra

III. Akkor is érvényes eredeti meggondolásunk, ha

P

és

R

eleve a kör egy átmérőjének végpontjai voltak. Ekkor, bár

P R

(ill.

P' R'

) átmegy

O

-n, a fenti

A^{*}

B^{*}

egybeesik

O

-val, az

S A^{*} B^{*}

már elfajult háromszög lenne, ekkor ‐ amint a II. esetben is ‐ minden valódi beírt háromszög kerülete határozottan nagyobb a

P R

szakasznál (3. ábra).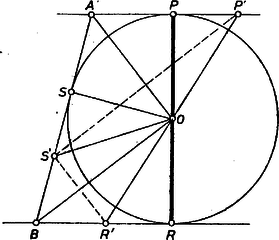

3. ábra

Megjegyzés. Bizonyításunk lényegében megegyezik Fejér Lipót magyar matematikusnak (1880‐1959) azzal a híres, egyszerű bizonyításával, ¹ amellyel megmutatta, hogy a hegyesszögű háromszögbe beírt háromszögek között van legkisebb területű és ez a háromszög talpponti háromszöge. ‐ Nyilvánvaló ugyanis, hogy

O S

O A B

háromszög magasságvonala, megmutatjuk még, hogy

A A^{*}

is merőleges

O B

-re. Az

O P R

egyenlő szárú háromszögben

P O R ∢ = P O A ∢ + A O B ∢ + B O R ∢ = A O S ∢ + A O B ∢ + S O B ∢ = 2 A O B ∢

, ezért

P R O ∢ = 90^{\circ} - A O B ∢

, és így

P R B ∢ = A^{*} R B ∢ = A^{*} S B ∢ = A O B ∢ = A O A^{*} ∢

. Így pedig

O

A

S

A^{*}

egy körön vannak, és

O S ⊥ A S

miatt e körben

O A

átmérő, ennélfogva

O A^{*} A ∢ = 90^{\circ}

. Ugyanígy

B B^{*} ⊥ O A

¹Lásd pl.:H. Rademacher ‐ O. Toeplitz: Számokról és alakzatokról, 2. kiadás, Középiskolai Szakköri Füzetek, Tankönyvkiadó, Budapest, 1954, 26‐30. o.