| Feladat: | 1238. matematika gyakorlat | Korcsoport: 14-15 | Nehézségi fok: - |
| Füzet: | 1970/január, 19 - 20. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Kör (és részhalmaza), mint mértani hely, Parabola, mint mértani hely, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1969/január: 1238. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Legyen először a szakasz egy belső pontja, egy körüli kör, melyre nézve külső pont, és az -ból -hoz húzott egyik érintő érintési pontja . Ekkor a pontból az szakasz derékszög alatt látszik. Tegyük fel egyelőre, hogy nincs rajta a egyenesen, azaz nem azonos -nak ezen az egyenesen levő vetületével. A egyenes metszi a szakaszt (éppen -ban), tehát elválasztja a , pontokat. Tegyük fel, hogy a -vel azonos oldalon van, így a egyenes az szakaszt nem metszi, az -t igen. Az szög tehát hegyesszög, az szög tompaszög. Hasonló módon kapjuk, hogy ha a -vel van azonos oldalon, akkor hegyesszög, és tompaszög. Összefoglalva a két esetet, azt mondhatjuk, hogy -ből az , szakaszok egyike hegyesszög, másika tompaszög alatt látszik. 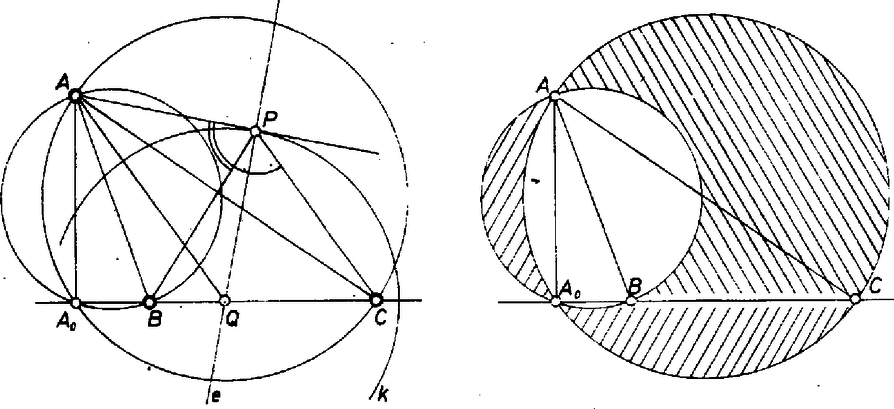 Vegyük most fel -t úgy, hogy csak az előbb kapott tulajdonság teljesüljön rá (de ne legyen rajta az egyenesen); megmutatjuk, hogy ekkor a mértani helyhez tartozik. Mondjuk az szakasz látszik -ből hegyesszög alatt, és tompaszög. Legyen az -re -ben emelt merőleges. Ekkor egyik félegyenese az szögtartomány belsejében halad és metszi az szakaszt, viszont az szögtartományon kívül halad, tehát -t nem metszi. Így az és pontok egyik oldalán, a másik oldalon helyezkedik el, metszi a szakaszt. Jelöljük a metszéspontot -val, így a körüli, -n átmenő kört az egyenes -ben érinti, tehát a keresett mértani helyhez tartozik. Azok a pontok, amelyekből tompaszög alatt látszik, az átmérőjű kör belsejében, amelyekből tompaszög alatt látszik, az átmérőjű kör belsejében vannak. A kapott pontok tehát azok, melyek e körök közül csak az egyikben vannak benne, de nincsenek rajta a egyenesen. Könnyű belátni, hogy csak akkor lehet a egyenesen, ha -lal azonos, és nyilván a mértani helyhez tartozik. A , illetve körüli körökhöz tartozó érintési pontok pedig , illetve kerületén vannak, maga a és pont természetesen egyikhez sem számítható hozzá. (De az és igen ‐ és ha például rajta van -n ‐ vagyis azonos -lal ‐, akkor persze hozzátartozik a mértani helyhez.) Hagyjuk el tehát a , körvonalakból a és pontokat, a keresett mértani hely a kapott ívek és az általuk határolt tartományok egyesítése lesz, kivéve belőle a két tartomány közös részét. |