Kezdőlap


Feladat:	1232. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balogh Zoltán
Füzet:	1969/november, 140 - 142. oldal		PDF \| MathML
Témakör(ök):	Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1968/december: 1232. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyenek az adott oldalszakaszok 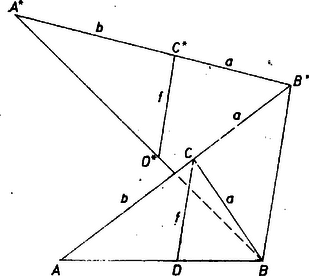$C B = a$ , $C A = b$ (ahol $a ≦ b$ ) és $C D = f$ .
Ötletet ad a szögfelező osztásarányára vonatkozó, ismert tétel bizonyításához használt ábra (1. ábra).

1. ábra

Mérjük rá

C A

-nak

C

-n túli meghosszabbítására a

C B^{*} = C B = a

szakaszt, így

C B B^{*}

egyenlő szárú háromszög,

B^{*} B | | C D

A B^{*} B ▵ \sim A C D ▵

\begin{matrix} B B^{*} = D C \cdot \frac{A B^{*}}{A C} = f \frac{a + b}{b} . \end{matrix}

Ez az adatokból megszerkeszthető, és belőle az ábra rekonstruálható:

B B^{*} C

egyenlő szárú háromszög,

B B^{*} C D

trapéz, végül

B D

és

B^{*} C

metszéspontja

A

.
A szerkesztés helyességéhez meg kell mutatni, hogy az adódó

A C

szakasz hossza

b

. Valóban

\begin{matrix} A B^{*} : A C = B^{*} B : C D, \\ 1 + \frac{a}{A C} = \frac{B B^{*}}{C D} = 1 + \frac{a}{b} . \end{matrix}

A szerkesztés végrehajtható, ha

B B^{*} < 2 a

, amit

f

-re megoldva

\begin{matrix} f < \frac{2 a b}{a + b} . \end{matrix}

(1)

Az ábrán

A^{*} C^{*} = b

C^{*} B^{*} = a

C^{*} D^{*} = f

, és a

B^{*}

-on átmenő,

C^{*} D^{*}

-gal párhuzamos egyenesnek

A^{*} D^{*}

-gal való metszéspontja

B

Balogh Zoltán (Debrecen, Fazekas M. Gimn., I. o. t.)

II. megoldás. Az eddigi jelölések mellett jelöljük a

C D

-re

D

-ben emelt merőlegesnek az

A C

B C

egyenesen levő pontját

A'

-vel, ill.

B'

-vel. Az 1169. gyakorlatban¹ láttuk, hogy

A' C

a

és

b

szakaszok harmonikus középarányosa:

\begin{matrix} A' C = h = \frac{2 a b}{a + b}, \end{matrix}

ami

a

b

alapján (pl. az idézett helyen leírt eljárással) megszerkeszthető. Így az

A' B' C

egyenlő szárú háromszög is, és ebből a keresett

A B C

háromszög is könnyen előállítható.
Induljunk ki egy tetszőleges

X C Y

szögből: mérjük fel ennek a száraira a

C B_{0} = a

C A_{0} = b

szakaszokat (2. ábra).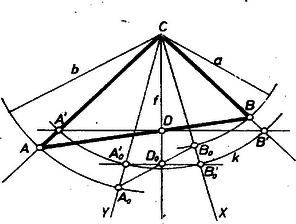

2. ábra

Jelöljük a szögfelező és

A_{0} B_{0}

metszéspontját

D_{0}

-lal, a

C D_{0}

-ra

D_{0}

-ban emelt merőlegesnek a szárakon levő pontjait

A'_{0}

-vel,

B'_{0}

-vel. Mérjük fel a

C D_{0}

szögfelezőre a

C D = f

szakaszt, és messe a

C D

-re

D

-ben emelt merőlegest a

C

középpontú,

C A'_{0}

sugarú

k

kör az

A'

B'

pontokban. Végül mérjük fel a

C A'

C B'

egyenesekre a

C A = b

C B = a

szakaszokat, a kapott

A B C

háromszög a keresett háromszög.
Szerkesztésünk helyességének bizonyításához csak azt kell megmutatnunk, hogy az

A B

oldalt a

C

-hez tartozó szögfelező

D

-ben metszi. Jelöljük ezt a metszéspontot

D_{1}

-gyel, az

A D_{1}

-re

D_{1}

-ben emelt merőlegesnek a szárakon levő pontjait

A'_{1}

-gyel,

B'_{1}

-gyel. Az 1169. gyakorlat szerint

\begin{matrix} A'_{1} C = h = \frac{2 a b}{a + b}, \end{matrix}

és ez szerkesztésünk szerint egyenlő

C A'_{0}

-vel.

A'_{1}

B'_{1}

tehát rajta van

k

-n, így rendre azonos

A'

-vel,

B'

-vel, amiből már következik, hogy

D_{1}

és

D

azonosak.

¹K. M. L. 37 (1968) 70. o. Másképpen

\begin{matrix} \frac{1}{h} = \frac{1}{2} (\frac{1}{a} + \frac{1}{b}) . \end{matrix}