Kezdőlap


Feladat:	1225. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Prőhle Tamás
Füzet:	1969/április, 161 - 162. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Nevezetes egyenlőtlenségek, Tetraéderek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1968/november: 1225. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek a tetraéder csúcsai $A$ , $B$ , $C$ , $D$ és $A B$ a leghosszabb éle vagy a leghosszabbak egyike. Megmutatjuk, hogy ennek valamelyik végpontjából induló $3$ élből szerkeszthető háromszög.
Három távolságból akkor szerkeszthető háromszög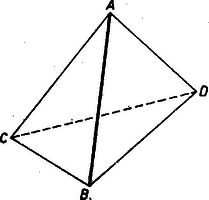, ha a legnagyobb is kisebb a másik kettő összegénél, hiszen a másik kettő már külön-külön is legfeljebb akkora lehet, mint a legnagyobb, tehát kisebb a másik két távolság összegénél.

Ha a tetraéder

A

-ból induló éleiből szerkeszthető háromszög, akkor állításunk helyes. Ha nem, ez csak úgy lehet, hogy

\begin{matrix} A B ≧ A C + A D . \end{matrix}

(1)

Viszont az

A B C

és

A B D

háromszögekből

\begin{matrix} A B < A C + C B és A B < A D + D B . \end{matrix}

A kettőt összeadva és (1)-et felhasználva

\begin{matrix} 2 A B < A C + C B + A D + D B ≦ A B + C B + D B, \end{matrix}

vagyis

\begin{matrix} A B < C B + D B, \end{matrix}

ez pedig azt jelenti, hogy az

A B

C B

D B

élekből szerkeszthető háromszög, mivel egyik él sem hosszabb

A B

-nél.

Prőhle Tamás (Budapest, Fazekas M. Gyak. Gimn., III. o. t.)

Megjegyzések. 1. Lehetséges, hogy a tetraédernek csak egyetlen csúcsából induló éleiből szerkeszthető háromszög, pl. ha az egyik lap szabályos háromszög és a többi él mindegyike a szabályos háromszög oldalának legalább kétszerese.
2. Nem használtuk fel a bizonyításban, hogy

A B ≧ C D

, tehát azt láttuk be, hogy ha a tetraéder egy éle nem kisebb a végpontjaiból induló élek egyikénél sem, akkor valamelyik végpontjából induló élekből szerkeszthető háromszög.