| Feladat: | 1221. matematika gyakorlat | Korcsoport: 14-15 | Nehézségi fok: nehéz |
| Megoldó(k): | Benkő L. , Fejes G. , Frankl P. , Gál P. , Gáspár Gy. , Hegyi F. , Horváth László , Horváth Márta , Kertész Á. , Kiss Ipoly , Láng I. , Lengyel J. , Orosz Éva , Pach J. , Sváb J. , Szendrei Ágnes , Temesvári T. , Turán Gy. | ||
| Füzet: | 1970/március, 108 - 109. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Egyenlő szárú háromszögek geometriája, Szögfelező egyenes, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1968/október: 1221. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Tetszés szerinti egyenlő szárú háromszögből kiindulva származtassuk a pontot a feladat előírása szerint, pedig jelölje az egyenes metszéspontját a egyenesnek az szög szögfelező egyenesére, -re vett tükörképével, amennyiben létrejön a metszéspont. 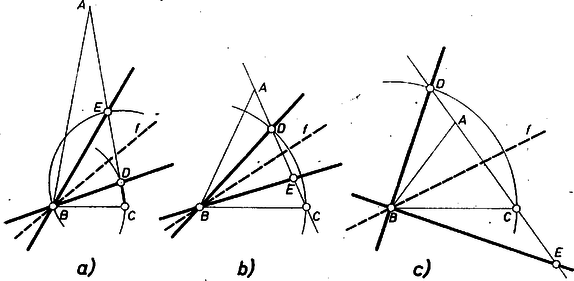 Megmutatjuk, hogy ekkor az háromszög egyenlő szárú. Ez tartalmazza a feladat állítását. A pont a félegyenesen van, mivel az szög hegyesszög, és szerkesztés szerint a háromszög egyenlő szárú, továbbá -nél levő szöge közös az háromszögével, így -t ugyanakkora és ugyanolyan irányú forgás viszi át -be, mint -t -be. Másrészt a egyenes tükörképe -re a egyenes, -é pedig a szerkesztés szerint a egyenes. -t tehát egyenlő nagyságú, de ellentétes irányú forgással vihetjük át -be, mint -t -be s ugyancsak mint -t -be. Ez azonban azt jelenti, hogy az és egyenesek az -szakasszal, annak ugyanazon oldalán egyenlő szöget zárnak be, s így az háromszög egyenlő szárú. Ezzel a feladat állítását ‐ sőt annál többet is ‐ bebizonyítottuk, kérdés azonban, mond-e valamit a feladat állítása, van-e olyan háromszög, amelyben kimetszhető az egyenesből a körüli sugarú körrel is. Ez esetben a háromszögben , ami akkor és csak akkor teljesül, ha
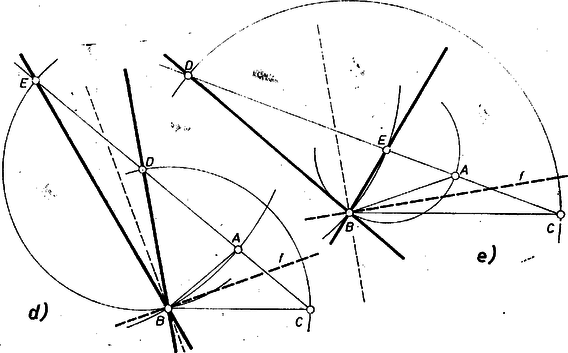 Hasonlóan elvégezve a számítást az ábra többi részénél a b) és c) esetben adódik (ekkor egybeesik -val, pedig -vel), a d) esetben , az e) esetben pedig . Így olyan háromszög-alak van, amelynél a feladat feltételei teljesülnek. |