Feladat: 1212. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Balogh Zoltán ,  Reviczky János ,  Tegze Miklós 
Füzet: 1969/május, 207 - 209. oldal  PDF  |  MathML 
Témakör(ök): Sakktáblával kapcsolatos feladatok, Gyakorlat
Hivatkozás(ok):Feladatok: 1968/szeptember: 1212. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. a) Elég megállapítani a kezdőpontból a célba vivő és hozzá állandóan közeledő, egymástól különböző útvonalak számát, hiszen minden egyes útvonalon pontosan 1-féleképpen haladhat végig a bástya: minden egyes lépését az útvonal egy-egy irányváltozása előtt fejezve be. Pl. az 1. ábra mindkét útvonalán 5 lépésben ér célba a bástya, lépéseinek hossza egymás után 2, 1, 2, 6, 3, ill. 5, 3, 1, 4, 1 mezőhossz.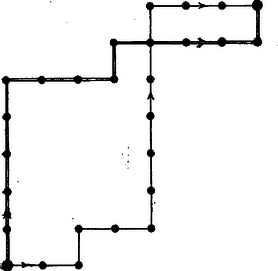

 

 

1. ábra
 

Az előírások miatt a tábla bal szélső oszlopának, valamint alsó sorának mezőire csak alsó, ill. bal szomszéd mezejükön át érkezhetünk, vagyis 1 féleképpen. Ezt fejezi ki a 2. ábra sakktáblájának megfelelő mezőire írt 1-es szám. A többi mezőkre alsó és bal szomszéd mezejükön át egyaránt érkezhetünk, és minden mezőre annyi útvonal vezet a kezdőpontból, amennyi a mondott két szomszéd (előbb átlépendő) mezőre vezető útvonalak számának összege. Az összegeket soronként fölfelé és balról jobbra haladva írtak be a mezőkre. A cél-mezőbe történt ‐ utolsó ‐ bejegyzés szerint az útvonalak ‐ és a bástya menetmódjainak ‐ száma 3432.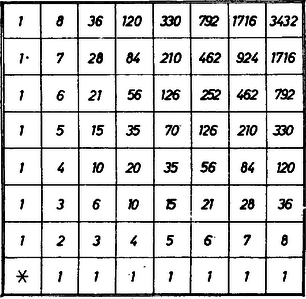
 

 

2. ábra
 

b) Az 1. ábra két 5-lépéses példája szerint a sakktábla 1. és 8. sora, ill. oszlopa közti 7‐7 lépésnyi szélességet és magasságot 3 és 2, ill. 2 és 3 lépésben teszi meg a bástya: 2+2+3=1+6=7, ill. 5+1+1=3+4=7. (A dűlt számjegyek a vízszintes lépések.) Valóban, mivel az előírt 5-ös lépésszám páratlan, azért a két irányú lépések száma különböző, másrészt a lépések váltakozó iránya miatt a különbség legföljebb 1 lehet.
Először azt állapítjuk meg, hogy 7 mezőnyi hosszúságot 2, ill. 3 darabban hányféleképpen tehet meg a bástya. Könnyű belátni, hogy 2 darabban 6-féleképpen, mert a 2.,3.,...,7. sorok (ill. oszlopok) közül pontosan egyben meg kell állnia, és ezt a sort 6-féleképpen lehet választani. (A példákban a 2. sor, ill. a 4. oszlop.)
3 darabban 2 különböző megállóhelyet kell választani a 6 közül. Ha mármost először a
2.,3.,4.,5.,6.
oszlopban állunk meg, a második megállóhely rendre
5,4,3,2,1
-féleképpen választható, mert ennyi a 8. oszlop és az elsőnek választott megálló oszlopa közti, további oszlopok száma. (Az első megálló most nem választható a 7. oszlopban.) A talált számok összege 15.
Az 5-lépéses menetmódok száma ezek alapján 15⋅6⋅2=180. Ugyanis minden ilyet úgy kapunk, hogy a tábla szélességét 3 darabban megtevő 15 lehetőség mindegyikébe ‐ a megállóhelyekben ‐ közbeiktatjuk a magasság 2 darabban való megtételének mindegyikét, egy-egy lépését, végül 2-vel szorzunk, mert mindegyik menetmódban felcserélhetjük a szélességet a magassággal. Az 1. ábra két példájában 7-nek a 2+2+3 és 1+6, ill. 5+1+1 és 3+4 három- és kéttagú felbontásait ágyaztuk egymásba.
 Balogh Zoltán (Debrecen, Fazekas M. Gimn., I. o. t.)
 Tegze Miklós (Budapest, VI., Hegedű utcai Ált. Isk., 8. o. t.)
 

Megjegyzések. 1. A 2. ábra táblázatából megtakaríthatjuk a jobbra lejtő átlótól jobbra eső mezők (nagyobb számokkal való) betöltését. Ugyanis a sakktábla szimmetrikus erre az átlóra és ennél a szimmetriánál a kezdő és a célmező szimmetrikus helyzetű, így az átló minden mezejébe a végpontból ugyanannyi út vezet (visszafelé), mint a kezdőpontból, és mindegyiket mindegyikkel összekapcsolva megkapjuk az illető állás mezőn áthaladó útvonalakat. Mindegyik átlós mezőt így sorra véve minden útvonalat számbaveszünk és mindegyiket egyszer, hiszen minden útvonal a mondott átlónak egy és csak egy mezején halad át. Eszerint az útvonalak száma az átlós mezőkbe beírt számok négyzetösszege, ami az átló számainak a jobbra emelkedő átlóra való szimmetriáját is figyelembe véve
2(12+72+212+352)=3432.
(Az utolsó meggondolás mutatja, hogy elég lett volna kitölteni a táblának csak a két átló alatti és az átlók alsó felében levő mezőit.)
 Reviczky János (Budapest, I. István Gimn., I. o. t.)
 

2. A b) kérdésre adott, választ a legtöbben az alábbiak szerint kapták. 7-nek 2, ill. 3 természetes szám összegére való felbontásai, a tagokat egyelőre nem-csökkenő rendben felsorolva:
7=1+6=2+5=3+4,ill.7=1+1+5=1+2+4=1+3+3=2+2+3.

A 3 kéttagú bontás mindegyike fordított sorrendben is használható, ezért a kéttagú felbontások összes száma 6.
A háromtagúak közül 1+2+4-et 3⋅2=6 különböző sorrendben írhatjuk fel, mert az elsőként elhelyezkedő tag (pl. az 1-es) helyének sorszámát 3-féleképpen választhatjuk meg, a másodszor elhelyezendőét a maradó helyek közül 2-féleképpen, ekkor pedig az utolsóként leírandó tag sorszáma a még nem választott sorszám.
A további 3 háromtagú felbontás két-két egyenlő tagot tartalmaz, az ezektől különböző tag (5, 1, ill. 3) helye most is 3-féleképpen választható, és ezzel a sorrend meg van határozva. Eszerint a 7 háromtagú felbontásainak száma 3+6+3+3=15.
3. Hasonlóan kaphatjuk, hogy a bástya
2,3,4,6,7,8
lépéssel
2,12,72,450,600,800
különböző módon érhet célba, 9,10,17,...,14 lépéssel pedig annyi módon, ahányféleképpen 7,6,5,...,2 lépéssel. Ugyanis pl. minden 11 lépéses menetmódhoz hozzárendelhető egy 2⋅8-11=5 lépéses ‐ és viszont ‐, ti. az, amelyben azokban és csak azokban a sorokban (oszlopokban) van megállóhely, amelyekben az 5 lépéses menetmódban nem álltunk meg.
 

II. megoldás. a) Minden az I. megoldás szerinti útvonalat leírhatunk 7‐7 db j, ill. f betű, azaz 14 jel felsorolásával, ahol j a jobbra, f a fölfelé való lépést jelenti, és fordítva, minden ilyen 14 tagú betűsorozat egyértelműen meghatároz egy menetvonalat. Ezért elég meghatározni az ilyen felsorolások számát. Pl. az 1. ábrán egy tollú nyíllal jelölt útvonal:
j,j,f,j,j,f,f,f,f,f,f,j,j,j.
Még ezt is egyszerűsíthetjük, csak azt mondva meg, hogy az 1.,2.,...,14. helyek közül melyeken áll pl. j jel, vagyis a példát folytatva ezt felírni:
1,2,4,5,12,13,14.

E 7 sorszámot egy megfelelő zacskóból húzva ki, a 7 cédula egymás utáni megválasztására 14,13,,...,,9,8 lehetőség van, és a teljes húzás különböző lehetőségeinek száma e számok szorzata.
Így azonban minden menetvonal ismételten kiadódik, a példabelire vezet többek közt ez a húzás is: 12,5,2,14,1,13,4. Az előbbihez hasonló meggondolás adja, hogy ez a 7-tagú számcsoport, és bármely más is az 1,2,...,14 számok közül 7⋅6⋅5⋅4⋅3⋅2 különböző sorrendben adódhat. Ezért a lehetőségek ‐ és a bástya keresett menetmódjainak száma a kapott két szorzat hányadosa:
14⋅13⋅12⋅11⋅10⋅9⋅87⋅6⋅5⋅4⋅3⋅2=2⋅13⋅2⋅11⋅2⋅3=23⋅3⋅11⋅13=3432.

b) Ugyanez a meggondolás könnyen kiadja az I. megoldás b) részében felhasznált 15-ös számot: a 6 sor (vagy oszlop) közül a megállóhelyet tartalmazó 2 sor megválasztási lehetőségeinek száma
6⋅52=15.
Ugyanígy 3 megállóhelyet
6⋅5⋅43⋅2=20
-féleképpen lehet választani; 4 és 5 megállót pedig annyiféleképpen, ahányféleképpen 3-at, ill. 2-t elhagyni lehet, vagyis elhagyásra kiválasztani, tehát ismét 15, ill. 6-féleképpen. Ezekből gyorsan adódik a 2,3,4;6,7,8 lépéses menetmódoknak a fenti 3. megjegyzésben közölt száma: 4 2⋅1⋅1=2, 2⋅6⋅1=12, 2⋅6⋅6=36; ill.
2⋅15⋅15=450,2⋅15⋅20=600,2⋅20⋅20=800.