Kezdőlap


Feladat:	1209. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Csetényi A. , Dombi G. , Donga Gy. , Feindl F. , Fischer Ágnes , Fodor P. , Frey Julianna , Gál P. , Gáspár Gy. , Gatter J. , Gerhardt T. , Gyimesi András , Gyimesi Ferenc , Göndőcs F. , Hegyi Gy. , Hetzer J. , Horváth L. , Klebnitczki J. , Komjáth P. , Kováts Annamária , Kuhár János , Lengyel J. , Magyar Árpád , Magyar László , Martoni V. , Máté A. , Mersich K. , Mihály Gy. , Reviczky J. , Sailer K. , Schügerl Márta , Simon Júlia , Skopál I. , Sváb J. , Szőke Mária , Viszkei Gy. , Zágon Katalin , Zámolyi F.
Füzet:	1969/február, 67 - 69. oldal		PDF \| MathML
Témakör(ök):	Numerikus és grafikus módszerek, Terület, felszín, Gyakorlat
Hivatkozás(ok):	Feladatok: 1968/május: 1209. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) Az egyes kecskék által lelegelhető mezőrészek nem nyúlnak egymásba, ha a három lánc leerősítési pontja céljára pl. egy a legelőt határoló $k$ körbe írt szabályos $A B C$ háromszög csúcspontjait választjuk ‐ és persze a láncok hosszát úgy, hogy mindegyik kecske valóban csak $1 / 4$ részét érje el a legelőnek. Megmutatjuk ugyanis, hogy az $A$ , $B$ és $C$ körül egymással páronként érintkező és egyenlő sugarú ‐ vagyis $A B / 2$ sugarú ‐ körök $k$ -ból ennek $1 / 4$ részénél nagyobb területet fednek le. Ezt tudva az már nyilvánvaló, hogy az $A$ , $B$ , $C$ középpontokat változatlanul hagyva, a sugarat viszont $A B / 2$ -nél kisebbre véve található olyan $ϱ$ sugár, hogy az $A$ (valamint $B$ , ill, $C$ ) körüli, $ϱ$ sugarú kör a legelő $1 / 4$ részét fedi le, és nincs átfedés.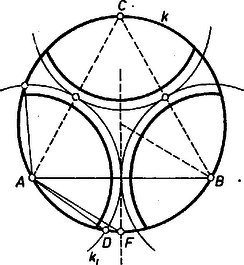

1. ábra

Messe az

A

közepű,

A B / 2

sugarú

k_{1}

k

-t a rövidebb

A B

ív

D

pontjában. Ez nincs rajta az

A B

húron, ennélfogva a húr felező merőlegesének

A

-t tartalmazó oldalán van, ezért ‐ az

A B

ív felezőpontját

F

-fel jelölve (

1

. ábra)

\begin{matrix} D A B ∢ > F A B ∢ = 30^{\circ}, \end{matrix}

tehát a

k_{1}

-nek

k

belsejében haladó ívéhez tartozó középponti szög nagyobb

120^{\circ}

-nál, ezért

k_{1}

területének a

k

belsejébe eső

t

része nagyobb, mint területének

1 / 3

része:

\begin{matrix} t > \frac{1}{3} π {(\frac{A B}{2})}^{2} . \end{matrix}

A jobb oldal pedig éppen

k

területének

1 / 4

része:

\begin{matrix} \frac{π}{12} A B^{2} = \frac{π}{12} \cdot 3 R^{2} = \frac{π R^{2}}{4}, \end{matrix}

ahol

R

k

sugara; ugyanis egyszerű számítás szerint

A B = R \sqrt[]{3}

.
b) Legyen a lánc kérdéses hossza

ϱ

, az

A

körüli,

ϱ

sugarú kör és

k

két metszéspontja

M

és

N

k

középpontja

O

M N

felezőpontja

G

, és

A O M ∢ = x

(fokban mérve;

2

. ábra), az utóbbit fogjuk közelítően meghatározni.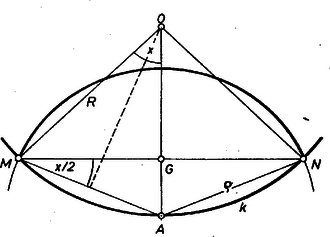

2. ábra

A kecske által elérhető legelőrészt az

A M

A N

szakaszok az általuk

k

-ból lemetszett körszeletekre és az

A M N

körcikkre osztják, az előbbieket pedig úgy kapjuk, hogy az

O M N

körcikkből elhagyjuk az

O M A N

deltoid területét. Nyilvánvalóan

M A N ∢ = 180^{\circ} - x

, így a követelmény, a szimmetriát felhasználva

\begin{matrix} ϱ^{2} π \cdot \frac{180^{\circ} - x}{360^{\circ}} + R^{2} π \cdot \frac{2 x}{360^{\circ}} - O A \cdot M G = \frac{1}{4} R^{2} π, \end{matrix}

ahol

M G = R sin x

, és

ϱ = 2 R sin x / 2

. Az első tagban az

A M G

derékszögű háromszög felhasználásával egyszerűsítést ad a következő alakítás:

\begin{matrix} ϱ^{2} = 2 R ϱ sin \frac{x}{2} = 2 R \cdot A G = 2 R (O A - O G) = 2 R^{2} (1 - cos x), \end{matrix}

hiszen a kerületi szögek tétele szerint

A M G ∢ = A M N ∢ = A O N ∢ / 2

. Egyenletünk így alakul:

\begin{matrix} (1 - \frac{x}{180^{\circ}}) cos x + \frac{sin x}{π} = \frac{3}{4}, \end{matrix}

és mivel a fentiek szerint

ϱ < R \sqrt[]{3} / 2

, ezért

\begin{matrix} sin \frac{x}{2} = \frac{ϱ}{2 R} < \frac{\sqrt[]{3}}{4} < 0, 4331, \frac{x}{2} < 25^{\circ} 40', x < 51^{\circ} 20' . \end{matrix}

A bal oldal értéke

x = 45^{\circ}

esetén

0, 7554

, nagyobb a jobb oldalnál,

x = 46^{\circ}

esetén pedig

0, 7461

, ez már kisebb.

x

keresett értéke a

0, 0054

többlet, ill.

0, 0039

hiány alapján

45^{\circ} 35'

körül várható.

ϱ / R

-nek a választott szögekhez tartozó értéke

0, 7654

, ill.

0, 7814

, így csak

77 %

és

78 %

jön szóba.

x = 45^{\circ} 35'

esetén az egyenlet bal oldala

0, 7500

, tehát ez a keresett szögérték, ehhez

ϱ / R = 0, 7748

, így

3

értékes jeggyel véve,

ϱ

R

-nek

77, 5 %

-a.

Kuhár János (Budapest, Berzsenyi D. Gimn., I. o. t.)