Feladat: 1206. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Ágoston Péter ,  Dombi Gábor ,  Donga György ,  Gyimesi András ,  Hetzer Jenő ,  Kacsuk Péter ,  Klebniczki József ,  Láz József ,  Prőhle Tamás ,  Reviczky János ,  Sailer Kornél ,  Simon Júlia ,  Szendrei Ágnes ,  Szendrei Mária ,  Várhegyi Éva ,  Viszkei Gy. 
Füzet: 1969/március, 108 - 110. oldal  PDF  |  MathML 
Témakör(ök): Kombinatorikus geometria térben, Gyakorlat
Hivatkozás(ok):Feladatok: 1968/május: 1206. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A szóban forgó test úgy állt elő az ABCD alapú és az AE, BF, CG, DH oldalélekkel meghatározott kockából, hogy kivágtuk belőle az ADGH és BCEF háromoldalú gúlákat (1. ábra).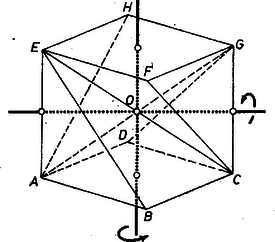

 

 

1. ábra
 

Láttuk, hogy a hálózat ragasztandó éleinek együttes hossza úgy lesz legrövidebb ‐ éppen 7 kockaélnyi, ha csak eredeti kockaéleket hagyunk meg ragasztandóknak, más szóval, ha a kocka 4 lapbeli átlójából és 2 térbeli átlójából keletkezett éleket a hálózaton a papír hajlításával állítjuk elő.
Eszerint az egymáshoz csatlakozó ABE, BEC, ECF és CFG háromszöglapok együttese egyben marad, és ugyanez áll a mondott lapoknak a kocka O középpontjára (a CE, AG átlók, ill. élek közös felezőpontjára) vonatkozó tükrös párjaiból alakuló együttesre. Nevezzük ezeket a lap-együtteseket lapkomplexeknek. Ezeket kiterítve, határvonaluk a kockaélnyi oldalhosszúságú ABCGFE=I, ill. CDAEHG=II egymással egybevágó, centrálisan szimmetrikus hatszög, melyeknek első három szöge (a csúcsok mondott rendjében) 90∘, 135∘, 135∘. Így csak azt kell vizsgálnunk, hogy a két komplex és az ABCD=III, EFGH=IV négyzet hányféleképpen kapcsolható össze hálózattá, vagyis hányféleképpen választható meg az a 3 kockaél (a testen maradt 10 közül), amelyet a papír hajtásával alakítunk ki.
Megjegyezzük, hogy az O-n átmenő, AE-vel párhuzamos egyenes a testnek forgási szimmetriatengelye, az e körüli 180∘-os elfordítás önmagába viszi át a testet, az (A, C), (B, D), (E, G), (F, H) csúcspárokat felcseréli, egyszersmind I-et is a II-vel. Ugyanilyen tengely az AE és CG élek felezőpontjain átmenő egyenes, az e körüli 180∘-os forgás egymásba viszi át a két komplexet, másrészt a két négyzetlapot is.
Először az olyan hálózatokat tekintjük, amelyekben I és II szomszédosak. Közös éleik, AE és CG a látott első szimmetriával egymásba átvihetők, elég tehát azt az esetet vizsgálnunk, amelyben a csatlakozó él AE (2. áb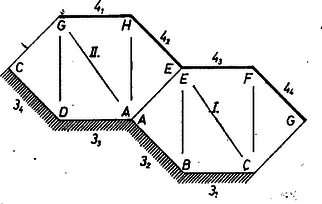ra).
 

 

2. ábra
 

Együttesük centrálisan szimmetrikus az AE szakasz K felezőpontjára. A III-as négyzetlap az ábra 31, 32, 33, 34 éleinek valamelyike mentén kapcsolódik, a IV-es lap pedig hasonlóan a 41, 42, 43, 44 élek valamelyike mentén. A csatlakozási élt egymástól függetlenül megválasztva 4⋅4=16 párosítás gondolható.
Ezek közül azonban ‐ ha i és j két különbözőt jelöl az 1, 2, 3, 4 indexek közül ‐ a 3i, 4j és a 3j, 4i párosítások nem különbözők, K körül egymásba fordíthatók. A 3i 4i választás viszont i minden értékére más hálózatot ad. Az utóbbi alakúak száma 4, a további 12 párosításból viszont csak fele, 6 különböző.
Továbbmenve, ha I és II nem szomszédos, akkor valamelyik négyzetlap mindegyikhez csatlakozik, a második szimmetria alapján erre elég III-at kiválasztanunk. I és II a III-hoz ennek vagy két szemben fekvő oldala mentén kapcsolódik, vagy két szomszédós oldala mentén. Az előbbire két különböző lehetőség van, ugyanis pl. az AB él nem egyenértékű a BC-vel, hiszen a testen különböző alakú lapok kapcsolódnak hozzájuk (3. és 4. ábra).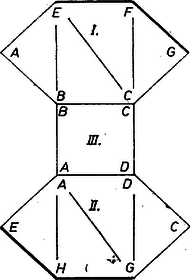
 

 

3. ábra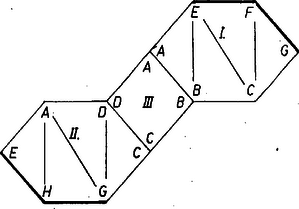
 
 

 

4. ábra
 

A I‐III lapok együttese mindkét esetben centrálisan szimmetrikus a III-as lap középpontjára nézve, és a IV-es lap csatlakozására alkalmas 4 él (vastagon rajzolva) is páronként egymás képe. Így a csatlakozási él mindkét ábrán 2-féleképpen választható meg.
Ha I és II a III-hoz ennek szomszédos oldalain csatlakoznak, e két oldal közös csúcsa csak A és C lehet ‐ hiszen pl. a BA, BC élek mindegyike mentén az I kapcsolódik III-hoz. Az első szimmetria miatt elég A-t vennünk közös csúcsnak (5. ábra).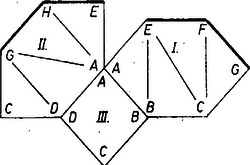
 

 

5. ábra
 

Az első három lap együttese így nem szimmetrikus, IV-et bármelyik lehetséges él mentén csatlakoztatva más-más hálózatot kapunk.
Mindezek szerint a lényegesen különböző hálózatok száma (4+6)+2+2+4=18. Felsoroljuk az ezekben hajtással képezett 3-3 kockaélt:
 

AE,  CB,  GH,   AE,  CB,  FG;   AB,  CD,  EF,AE,  BA,  HE,   AE,  BA,  EF,   AB,  CD,  FG;AE,  AD,  EF,   AE,  BA,  FG;   AB,  AD,  EF,AE,  DC,  FG;   AE,  AD,  FG;   AB,  AD,  FG,AE,  CB,  HE,   BC,  AD,  EF,   AB,  AD,  GH,AE,  CB,  EF,   BC,  AD,  FG;   AB,  AD,  HE.

 (Egy névtelen dolgozat felhasználásával)